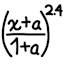sRGB transform library

Introduction

The sRGB standard defines a color space, and a non-linear transfer function that maps numerical values to linear intensities. In particular, sRGB maps 0.0 to pure black and 1.0 to the white point of the device, but the sRGB value of 0.5 is not half the physical brightness of white (in fact it is 21.4% as bright).

All popular computer displays and software use sRGB to represent colors, but doing image processing properly requires doing math in the linear domain. Hence conversions between sRGB and linear values are necessary for high-fidelity image processing.

While the sRGB transform formulas are short, they are not easy to remember and require some care to avoid subtle problems. This small library saves the effort of repeatedly writing sRGB conversion functions in every application program and verifying the correctness of each copy.

Source code

Java

SrgbTransform.java
SrgbTransformTest.java (JUnit)

C

C++

Python

TypeScript / JavaScript

srgb-transform.ts / srgb-transform.js

License: MIT (open source)

Math notes

The transforms are defined as follows:

\(\text{srgbToLinear}(x) = \begin{cases} x / 12.92 & \text{if }0.0 ≤ x ≤ 0.04045 \\ \left(\frac{x + 0.055}{1.055}\right)^{2.4} & \text{if } 0.04045 < x ≤ 1.0 \end{cases}.\)
\(\text{linearToSrgb}(x) = \begin{cases} 12.92x & \text{if }0.0 ≤ x ≤ 0.0031308 \\ 1.055 x^{1/2.4} - 0.055 & \text{if } 0.0031308 < x ≤ 1.0 \end{cases}.\)

The numerical constants in the formulas are inexact and lead to subtle consequences. The function srgbToLinear maps the input range [0.0, 0.04045] to the output range [0, 809/258400] = [0.0, 0.00313080495...], and maps the input range (0.04045, 1.0] to the output range ((1909/21100)^2.4, 1] = (0.00313080728..., 1.0]. This function is one-to-one (injective), but its output ranges have a tiny gap of (0.00313080495..., 0.00313080728...] of length ~2×10⁻⁹.

The function linearToSrgb maps the input range [0.0, 0.0031308] to the output range [0.0, 0.040449936], and maps the input range (0.0031308, 1.0] to the output range (0.04044990748..., 1.0]. Its two output ranges overlap in [0.04044993600, 0.04044990748...) with a length of ~3×10⁻⁸, making linearToSrgb not an one-to-one function.

For almost all values of x ∈ [0.0, 1.0], the two possible round-trip transforms from one space to the other space and back (e.g. sRGB-to-linear-to-sRGB) only yields tiny rounding errors based on the numerical precision (e.g. float vs. double). But for sRGB-to-linear-to-sRGB when x ∈ (0.040449936, 0.04045] (interval length 6.4×10⁻⁸), the result can have an error up to 3×10⁻⁸. Similarly for linear-to-sRGB-to-linear when x ∈ (0.0031308, 0.00313080728...] (interval length ~7×10⁻⁹), the result can have an error up to 3×10⁻⁹.

Because these formulas imply that both round-trip transforms are mathematically inexact on some values, applications should be designed to avoid sRGB/linear conversions as much as possible. For example, computer-generated graphics should process all aspects of a picture in linear color space, and at the last step convert to sRGB for image export.