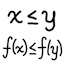 Public transit and monotonicity
Public transit and monotonicity
Suppose I’m commuting home during rush hour, waiting at a subway station. A crowded train arrives at the station and I have to decide: Should I try to squeeze myself into this train, or should I wait for the next one? If I take the crowded train, I might have to be quite rude to the other passengers to try to squeeze in, the train would probably remain crowded for much of the trip, and I would likely not have a place to sit down and rest. So if instead I wait for the next train, I might get a more comfortable ride[0], but my commute time would increase. Either way, I would make a choice simply based on the tradeoff of faster trip versus more comfortable trip. Departing earlier means arriving earlier, right? Well, there’s more than meets the eye...
In mathematics, a function f is called monotonic[1] if, informally speaking, it either only goes up or only goes down. For the case of a single variable function, suppose y = f(x). If increasing x always makes y stay the same or increase, then f is monotonic (example). Or if increasing x always makes y stay the same or decrease, then f is also monotonic (example). Otherwise, the function f is not monotonic (example).
Why is this mathematical concept relevant? If we treat the arrival time as a function of the departure time (i.e. tarrival = f(tdeparture)), then we can observe that some forms of transportation are monotonic[2] while others are not. Take trains for example. If trains run on a simple two-track rail line[3], then this mode of transportation is monotonic – trains going in the same direction cannot overtake each other, so the relative order is always maintained. In practice, this means at the point where you depart, taking an earlier train means you will arrive at the destination point earlier; it is impossible to take a later train at the departure point and arrive earlier. Trams and streetcars are also monotonic for the same reason, and buses on one-lane-per-direction roads are mostly monotonic too.
By contrast, buses on a road with at least 2 lanes will frequently behave non-monotonically. If one bus needs to stop to pick up a passenger but the bus behind does not need to stop, then the bus behind can overtake and will now become the bus in front. Also, a bus or train system where there are different classes of service – such as local service vs. express service – are clearly not monotonic: Even if a local bus departs before an express bus by a few minutes, the express bus will likely overtake the local bus by the end of the route.
As for personal transportation instead of public transport, the modes are fairly monotonic. For walking and bicycling, generally there are no significant factors for making them non-monotonic. For driving, it is mostly monotonic – except for things like time-dependent routing: Suppose a car accident would happen on some road at 09:10. If you departed at 09:00, you might get stuck immediately behind the location of the accident. If you departed at 09:20, you might have noticed a congestion further upstream and took a detour to entirely avoid the slowdown.
The first conclusion of this analysis is that on some transportation systems, departing earlier definitely means arriving earlier; on other systems this is not always true. The second conclusion is that if the transportation system you’re using is monotonic, then the only question you need to ask yourself is “Do I want to get there faster, or do I think it’ll be more comfortable to wait a bit?”. Otherwise if the system is not monotonic, then you need to consider additional factors such as “Will the local bus depart early enough to still beat the express bus?”.
Notes
[0]: Even during rush hour, the density of trains fluctuates – it is possible for one train to be packed completely full and the next to be half empty. This is generally due to the trains being spaced non-uniformly in time. For example, the full train might have picked up 10 minutes’ worth of passenger accumulation at the station, while the half-empty train might have picked up only 2 minutes’ worth of accumulation.
[1]: The words monotonic/monotonicity (a function moving in only one direction) is not to be confused with the words monotonous/monotony/monotonousness (boring).
[2]: To use words more precisely but stiffly: “... some forms of transportation are characterized by a monotonic time function ...”
[3]: With no crossover switches, detour tracks, etc.