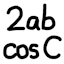Numerically stable law of cosines

Introduction

The law of cosines: \(c^2 = a^2 + b^2 - 2ab \cos C\).

This trigonometric equation relates four values in a triangle – the three side lengths and one angle. Depending on which variables you know, you can solve the equation for a side or for an angle.

However when this formula is implemented straightforwardly in computer floating-point arithmetic, some situations will yield highly inaccurate results. When the given triangle is very long and skinny, the numerical result is inaccurate (large relative error) due to intermediate calculations that subtract very similar numbers.

This article explains how to modify the law of cosines to calculate accurately in these situations, giving mathematical derivations to alternative formulas that can be implemented. (In fact they are implemented on my JavaScript triangle solver page already.)

Solving for side

From the law of cosines formula, this should be clear: \(c = \sqrt{a^2 + b^2 - 2ab \cos C}\).

If \(a \approx b\) (they have similar magnitudes) and angle \(C \approx 0\) (close to zero), then \(\cos C \approx 1\).
Hence \(a^2 + b^2 - 2ab \cos C \:\approx\: a^2 + a^2 - 2a^2 \cos 0 \:\approx\: 2a^2 - 2a^2 \:\approx\: 0\).
Therefore \(c \approx \sqrt{0} \approx 0\). But \(c\) could be a small number like \(10^{-20}\), which is still representable in floating-point.

We can do better than this. The Taylor series expansion of the cosine function (for \(C\) in radians) yields: \(\cos C = 1 - \frac{C^2}{2!} + \frac{C^4}{4!} - \cdots\).

Then \(a^2 + b^2 - 2ab \cos C\)
\(= a^2 + b^2 - 2ab (1 + \cos C - 1)\)
\(= (a^2 + b^2 - 2ab) - 2ab (\cos C - 1)\)
\(= (a^2 - 2ab + b^2) - 2ab \left(-\frac{C^2}{2!} + \frac{C^4}{4!} - \cdots\right)\)
\(\approx (a - b)^2 + 2ab \left(\frac{C^2}{2!} - \frac{C^4}{4!}\right)\)
\(=(a - b)^2 + ab C^2 \left(1 - \frac{C^2}{12}\right)\).

Therefore our numerically stable formula is \(c \approx \sqrt{(a - b)^2 + ab C^2 \left(1 - \frac{C^2}{12}\right)}\), empirically suitable for \(|C| < 10^{-3}\).

Notes:

Both terms of the sum are positive, so only the difference \(a - b\) needs to be examined for possible cancellation.
If \(a \approx b\) then their difference can be represented exactly in floating-point numbers, so there is no problem.
If \(a\) and \(b\) differ by a lot, it’s still okay because the final result will still be much larger than the error, thus maintaining a small relative error.

Solving for angle

Rearranging the law of cosines formula, we get: \(C = \cos^{-1}\! \left(\frac{a^2 + b^2 - c^2}{2ab}\right)\).

When side \(c \approx 0\) (which also implies \(a \approx b\)), we should have angle \(C \approx 0\). But \(\cos C = \frac{a^2 + b^2 - c^2}{2ab} \approx 1\), and numbers very close to \(1\) will be rounded to \(1\). This means \(\cos^{-1}\! \left(\frac{a^2 + b^2 - c^2}{2ab}\right)\) will be exactly \(0\) instead of a small number like \(10^{-20}\) which is still representable in floating-point.

By using the Taylor expansion again, we can derive the following approximation:
Assume that \(x \approx 0\) and \(y \approx 1\). Then \(y = \cos x \approx 1 - \frac{x^2}{2}\). Thus \(x \approx \sqrt{2 - 2y}\).

Now let’s avoid calculating the subformula \(a^2 + b^2 - c^2\) because it subtracts a tiny value \(c^2\) from a huge value \(a^2 + b^2\) (which is a different type of cancellation):
\(C \approx \sqrt{2 - 2\left(\frac{a^2 + b^2 - c^2}{2ab}\right)}\)
\(= \sqrt{2 - \frac{a^2 + b^2 - c^2}{ab}}\)
\(= \sqrt{\frac{2ab - a^2 - b^2 + c^2}{ab}}\)
\(= \sqrt{\frac{c^2 - (a-b)^2}{ab}}\).

Therefore our numerically stable formula is \(C \approx \sqrt{\frac{c^2 - (a-b)^2}{ab}}\), which is empirically suitable for when the arccosine argument \(\frac{a^2 + b^2 - c^2}{2ab} > 1 - 10^{-8}\) or equivalently \(\frac{c^2 - (a-b)^2}{2ab} < 10^{-8}\).

Numerical comparison

Setup notes:

The sides \(a\) and \(b\) are set to \(10^8\) in all cases. The angle \(C\) is in radians.
The “naive” and “stable” algorithms used IEEE 754 double precision for storage and arithmetic, as well as Java’s math library for sqrt(), cos(), and acos().
The “precise” computation was performed in a computer algebra system with arbitrary precision arithmetic. The relative errors were also computed precisely in the CAS.
The naive and stable results are printed with 17 correctly rounded significant figures; the precise results are printed with 25 correct sig figs.

Solving for side:

\(C\)	\(c\) (naive)	\(c\) (stable)	\(c\) (precise)	Naive rel err	Stable rel err
8.254×10⁻⁰¹	8.0217203041092455×10⁺⁷	8.0163093884354800×10⁺⁷	8.0217203041092457453923973×10⁺⁷	−2.58×10⁻¹⁷	−6.75×10⁻⁴
3.831×10⁻⁰¹	3.8077989132683828×10⁺⁷	3.8076838697627425×10⁺⁷	3.8077989132683806640465265×10⁺⁷	+5.73×10⁻¹⁶	−3.02×10⁻⁵
1.778×10⁻⁰¹	1.7759372471968371×10⁺⁷	1.7759347755013548×10⁺⁷	1.7759372471968379146724865×10⁺⁷	−4.35×10⁻¹⁶	−1.39×10⁻⁶
8.254×10⁻⁰²	8.2516989633582728×10⁺⁶	8.2516984311624831×10⁺⁶	8.2516989633581144029010656×10⁺⁶	+1.92×10⁻¹⁴	−6.45×10⁻⁸
3.831×10⁻⁰²	3.8309525449705063×10⁺⁶	3.8309525335063864×10⁺⁶	3.8309525449707342923629298×10⁺⁶	−5.95×10⁻¹⁴	−2.99×10⁻⁹
1.778×10⁻⁰²	1.7782559792425837×10⁺⁶	1.7782559789960068×10⁺⁶	1.7782559792429917482831550×10⁺⁶	−2.29×10⁻¹³	−1.39×10⁻¹⁰
8.254×10⁻⁰³	8.2540184218112822×10⁺⁵	8.2540184217583749×10⁺⁵	8.2540184218115887490007133×10⁺⁵	−3.71×10⁻¹⁴	−6.45×10⁻¹²
3.831×10⁻⁰³	3.8311845064418390×10⁺⁵	3.8311845064677182×10⁺⁵	3.8311845064688626372997494×10⁺⁵	−7.05×10⁻¹²	−2.99×10⁻¹³
1.778×10⁻⁰³	1.7782791757201680×10⁺⁵	1.7782791757300220×10⁺⁵	1.7782791757300465671183906×10⁺⁵	−5.56×10⁻¹²	−1.38×10⁻¹⁴
8.254×10⁻⁰⁴	8.2540416185042341×10⁺⁴	8.2540416183712921×10⁺⁴	8.2540416183713007562273147×10⁺⁴	+1.61×10⁻¹¹	−1.04×10⁻¹⁵
3.831×10⁻⁰⁴	3.8311868239489442×10⁺⁴	3.8311868261264004×10⁺⁴	3.8311868261263991925039066×10⁺⁴	−5.68×10⁻¹⁰	+3.18×10⁻¹⁶
1.778×10⁻⁰⁴	1.7782794156149928×10⁺⁴	1.7782794076958340×10⁺⁴	1.7782794076958339471918206×10⁺⁴	+4.45×10⁻⁹	+3.85×10⁻¹⁷
8.254×10⁻⁰⁵	8.2540419189630975×10⁺³	8.2540418503371002×10⁺³	8.2540418503370954020360420×10⁺³	+8.31×10⁻⁹	+5.80×10⁻¹⁶
3.831×10⁻⁰⁵	3.8311867613051704×10⁺³	3.8311868493229758×10⁺³	3.8311868493229788136203039×10⁺³	−2.30×10⁻⁸	−7.78×10⁻¹⁶
1.778×10⁻⁰⁵	1.7782789432482184×10⁺³	1.7782794100154920×10⁺³	1.7782794100154919126759159×10⁺³	−2.62×10⁻⁷	+3.57×10⁻¹⁷
8.254×10⁻⁰⁶	8.2540414343520229×10⁺²	8.2540418526567589×10⁺²	8.2540418526567533682467109×10⁺²	−5.07×10⁻⁸	+6.73×10⁻¹⁶
3.831×10⁻⁰⁶	3.8311878053679385×10⁺²	3.8311868495549419×10⁺²	3.8311868495549446102570243×10⁺²	+2.49×10⁻⁷	−7.11×10⁻¹⁶
1.778×10⁻⁰⁶	1.7783138080777533×10⁺²	1.7782794100386886×10⁺²	1.7782794100386884923399252×10⁺²	+1.93×10⁻⁵	+5.02×10⁻¹⁷
8.254×10⁻⁰⁷	8.2534841127853397×10⁺¹	8.2540418526799556×10⁺¹	8.2540418526799499479107929×10⁺¹	−6.76×10⁻⁵	+6.83×10⁻¹⁶
3.831×10⁻⁰⁷	3.8314488121336034×10⁺¹	3.8311868495572618×10⁺¹	3.8311868495572642682234341×10⁺¹	+6.84×10⁻⁵	−6.42×10⁻¹⁶
1.778×10⁻⁰⁷	1.7776388834631177×10⁺¹	1.7782794100389204×10⁺¹	1.7782794100389204581365662×10⁺¹	−3.60×10⁻⁴	−5.48×10⁻¹⁷
8.254×10⁻⁰⁸	8.2462112512353212×10⁺⁰	8.2540418526801869×10⁺⁰	8.2540418526801819137074339×10⁺⁰	−9.49×10⁻⁴	+6.00×10⁻¹⁶
3.831×10⁻⁰⁸	4.0000000000000000×10⁺⁰	3.8311868495572847×10⁺⁰	3.8311868495572874648030982×10⁺⁰	+4.41×10⁻²	−7.15×10⁻¹⁶
1.778×10⁻⁰⁸	2.0000000000000000×10⁺⁰	1.7782794100389228×10⁺⁰	1.7782794100389227777945326×10⁺⁰	+1.25×10⁻¹	−1.07×10⁻¹⁷
8.254×10⁻⁰⁹	0.0000000000000000×10⁻¹	8.2540418526801729×10⁻¹	8.2540418526801842333654003×10⁻¹	−1.00×10⁺⁰	−1.38×10⁻¹⁵
3.831×10⁻⁰⁹	0.0000000000000000×10⁻¹	3.8311868495572932×10⁻¹	3.8311868495572876967688948×10⁻¹	−1.00×10⁺⁰	+1.43×10⁻¹⁵
1.778×10⁻⁰⁹	0.0000000000000000×10⁻¹	1.7782794100389229×10⁻¹	1.7782794100389228009911123×10⁻¹	−1.00×10⁺⁰	+6.99×10⁻¹⁷
8.254×10⁻¹⁰	0.0000000000000000×10⁻²	8.2540418526801732×10⁻²	8.2540418526801842565619800×10⁻²	−1.00×10⁺⁰	−1.35×10⁻¹⁵
3.831×10⁻¹⁰	0.0000000000000000×10⁻²	3.8311868495572929×10⁻²	3.8311868495572876990885528×10⁻²	−1.00×10⁺⁰	+1.35×10⁻¹⁵
1.778×10⁻¹⁰	0.0000000000000000×10⁻²	1.7782794100389229×10⁻²	1.7782794100389228012230781×10⁻²	−1.00×10⁺⁰	+6.98×10⁻¹⁷
8.254×10⁻¹¹	0.0000000000000000×10⁻³	8.2540418526801732×10⁻³	8.2540418526801842567939458×10⁻³	−1.00×10⁺⁰	−1.35×10⁻¹⁵
3.831×10⁻¹¹	0.0000000000000000×10⁻³	3.8311868495572929×10⁻³	3.8311868495572876991117494×10⁻³	−1.00×10⁺⁰	+1.35×10⁻¹⁵
1.778×10⁻¹¹	0.0000000000000000×10⁻³	1.7782794100389225×10⁻³	1.7782794100389228012253978×10⁻³	−1.00×10⁺⁰	−1.50×10⁻¹⁶
8.254×10⁻¹²	0.0000000000000000×10⁻⁴	8.2540418526801725×10⁻⁴	8.2540418526801842567962654×10⁻⁴	−1.00×10⁺⁰	−1.42×10⁻¹⁵
3.831×10⁻¹²	0.0000000000000000×10⁻⁴	3.8311868495572923×10⁻⁴	3.8311868495572876991119813×10⁻⁴	−1.00×10⁺⁰	+1.21×10⁻¹⁵
1.778×10⁻¹²	0.0000000000000000×10⁻⁴	1.7782794100389227×10⁻⁴	1.7782794100389228012254210×10⁻⁴	−1.00×10⁺⁰	−5.83×10⁻¹⁷
8.254×10⁻¹³	0.0000000000000000×10⁻⁵	8.2540418526801736×10⁻⁵	8.2540418526801842567962886×10⁻⁵	−1.00×10⁺⁰	−1.29×10⁻¹⁵

Observations for the data above: The naive algorithm has less relative error when approximately \(C > 10^{-3}\) radians, because the stable algorithm truncates the cosine series. But for \(C\) below this, the stable algorithm is more accurate. Moreover, the naive algorithm completely falls apart when \(C < 10^{-8}\), always giving a result of 0 instead of a tiny positive number.

Solving for angle:

\(c\)	\(C\) (naive)	\(C\) (stable)	\(C\) (precise)	Naive rel err	Stable rel err
8.254×10⁺⁰⁷	8.5083716972718348×10⁻⁰¹	8.2540418526801895×10⁻⁰¹	8.5083716972718281127650820×10⁻⁰¹	+7.91×10⁻¹⁶	−2.99×10⁻²
3.831×10⁺⁰⁷	3.8550133141801396×10⁻⁰¹	3.8311868495572848×10⁻⁰¹	3.8550133141801425715491534×10⁻⁰¹	−7.72×10⁻¹⁶	−6.18×10⁻³
1.778×10⁺⁰⁷	1.7806308740167129×10⁻⁰¹	1.7782794100389226×10⁻⁰¹	1.7806308740167164643291790×10⁻⁰¹	−2.01×10⁻¹⁵	−1.32×10⁻³
8.254×10⁺⁰⁶	8.2563867392267828×10⁻⁰²	8.2540418526801898×10⁻⁰²	8.2563867392267940604361858×10⁻⁰²	−1.36×10⁻¹⁵	−2.84×10⁻⁴
3.831×10⁺⁰⁶	3.8314211971419307×10⁻⁰²	3.8311868495572853×10⁻⁰²	3.8314211971420579196363537×10⁻⁰²	−3.32×10⁻¹⁴	−6.12×10⁻⁵
1.778×10⁺⁰⁶	1.7783028417606830×10⁻⁰²	1.7782794100389229×10⁻⁰²	1.7783028417610801004879759×10⁻⁰²	−2.23×10⁻¹³	−1.32×10⁻⁵
8.254×10⁺⁰⁵	8.2540652837349952×10⁻⁰³	8.2540418526801732×10⁻⁰³	8.2540652837483225589699241×10⁻⁰³	−1.61×10⁻¹²	−2.84×10⁻⁶
3.831×10⁺⁰⁵	3.8311891926739367×10⁻⁰³	3.8311868495572929×10⁻⁰³	3.8311891926500117494692299×10⁻⁰³	+6.24×10⁻¹²	−6.12×10⁻⁷
1.778×10⁺⁰⁵	1.7782796442869352×10⁻⁰³	1.7782794100389228×10⁻⁰³	1.7782796443478916540907761×10⁻⁰³	−3.43×10⁻¹¹	−1.32×10⁻⁷
8.254×10⁺⁰⁴	8.2540420878769543×10⁻⁰⁴	8.2540418526801736×10⁻⁰⁴	8.2540420869890877114652504×10⁻⁰⁴	+1.08×10⁻¹⁰	−2.84×10⁻⁸
3.831×10⁺⁰⁴	3.8311868745189868×10⁻⁰⁴	3.8311868495572923×10⁻⁰⁴	3.8311868729881766356180823×10⁻⁰⁴	+4.00×10⁻¹⁰	−6.12×10⁻⁹
1.778×10⁺⁰⁴	1.7782794191261900×10⁻⁰⁴	1.7782794100389227×10⁻⁰⁴	1.7782794123820116645208938×10⁻⁰⁴	+3.79×10⁻⁹	−1.32×10⁻⁹
8.254×10⁺⁰³	8.2540419783121356×10⁻⁰⁵	8.2540418526801898×10⁻⁰⁵	8.2540418550232731135519455×10⁻⁰⁵	+1.49×10⁻⁸	−2.84×10⁻¹⁰
3.831×10⁺⁰³	3.8311867817738467×10⁻⁰⁵	3.8311868495572856×10⁻⁰⁵	3.8311868497915965846466533×10⁻⁰⁵	−1.78×10⁻⁸	−6.12×10⁻¹¹
1.778×10⁺⁰³	1.7782792544822105×10⁻⁰⁵	1.7782794100389229×10⁻⁰⁵	1.7782794100623536897758526×10⁻⁰⁵	−8.75×10⁻⁸	−1.32×10⁻¹¹
8.254×10⁺⁰²	8.2540462802021769×10⁻⁰⁶	8.2540418526801902×10⁻⁰⁶	8.2540418527036151453460663×10⁻⁰⁶	+5.36×10⁻⁷	−2.84×10⁻¹²
3.831×10⁺⁰²	3.8311925772508779×10⁻⁰⁶	3.8311868495572849×10⁻⁰⁶	3.8311868495596307879669473×10⁻⁰⁶	+1.50×10⁻⁶	−6.12×10⁻¹³
1.778×10⁺⁰²	1.7783023543096177×10⁻⁰⁶	1.7782794100389229×10⁻⁰⁶	1.7782794100391571101109173×10⁻⁰⁶	+1.29×10⁻⁵	−1.32×10⁻¹³
8.254×10⁺⁰¹	8.2536831045905480×10⁻⁰⁷	8.2540418526801902×10⁻⁰⁷	8.2540418526804185656817849×10⁻⁰⁷	−4.35×10⁻⁵	−2.77×10⁻¹⁴
3.831×10⁺⁰¹	3.8310766614027379×10⁻⁰⁷	3.8311868495572850×10⁻⁰⁷	3.8311868495573111300005333×10⁻⁰⁷	−2.88×10⁻⁵	−6.82×10⁻¹⁵
1.778×10⁺⁰¹	1.7756782901008428×10⁻⁰⁷	1.7782794100389230×10⁻⁰⁷	1.7782794100389251443142762×10⁻⁰⁷	−1.46×10⁻³	−1.23×10⁻¹⁵
8.254×10⁺⁰⁰	8.2966154259890665×10⁻⁰⁸	8.2540418526801902×10⁻⁰⁸	8.2540418526801865998851438×10⁻⁰⁸	+5.16×10⁻³	+4.35×10⁻¹⁶
3.831×10⁺⁰⁰	3.9424766765007238×10⁻⁰⁸	3.8311868495572849×10⁻⁰⁸	3.8311868495572879334208692×10⁻⁰⁸	+2.90×10⁻²	−8.02×10⁻¹⁶
1.778×10⁺⁰⁰	2.1073424255447017×10⁻⁰⁸	1.7782794100389228×10⁻⁰⁸	1.7782794100389228246563097×10⁻⁰⁸	+1.85×10⁻¹	−1.80×10⁻¹⁸
8.254×10⁻⁰¹	0.0000000000000000×10⁻⁰⁹	8.2540418526801727×10⁻⁰⁹	8.2540418526801842802271774×10⁻⁰⁹	−1.00×10⁺⁰	−1.41×10⁻¹⁵
3.831×10⁻⁰¹	0.0000000000000000×10⁻⁰⁹	3.8311868495572935×10⁻⁰⁹	3.8311868495572877014550725×10⁻⁰⁹	−1.00×10⁺⁰	+1.50×10⁻¹⁵
1.778×10⁻⁰¹	0.0000000000000000×10⁻⁰⁹	1.7782794100389230×10⁻⁰⁹	1.7782794100389228014597301×10⁻⁰⁹	−1.00×10⁺⁰	+1.28×10⁻¹⁶
8.254×10⁻⁰²	0.0000000000000000×10⁻¹⁰	8.2540418526801727×10⁻¹⁰	8.2540418526801842570305977×10⁻¹⁰	−1.00×10⁺⁰	−1.41×10⁻¹⁵
3.831×10⁻⁰²	0.0000000000000000×10⁻¹⁰	3.8311868495572929×10⁻¹⁰	3.8311868495572876991354146×10⁻¹⁰	−1.00×10⁺⁰	+1.37×10⁻¹⁵
1.778×10⁻⁰²	0.0000000000000000×10⁻¹⁰	1.7782794100389229×10⁻¹⁰	1.7782794100389228012277643×10⁻¹⁰	−1.00×10⁺⁰	+4.04×10⁻¹⁷
8.254×10⁻⁰³	0.0000000000000000×10⁻¹¹	8.2540418526801737×10⁻¹¹	8.2540418526801842567986319×10⁻¹¹	−1.00×10⁺⁰	−1.28×10⁻¹⁵
3.831×10⁻⁰³	0.0000000000000000×10⁻¹¹	3.8311868495572927×10⁻¹¹	3.8311868495572876991122180×10⁻¹¹	−1.00×10⁺⁰	+1.30×10⁻¹⁵
1.778×10⁻⁰³	0.0000000000000000×10⁻¹¹	1.7782794100389227×10⁻¹¹	1.7782794100389228012254446×10⁻¹¹	−1.00×10⁺⁰	−6.86×10⁻¹⁷
8.254×10⁻⁰⁴	0.0000000000000000×10⁻¹²	8.2540418526801727×10⁻¹²	8.2540418526801842567963123×10⁻¹²	−1.00×10⁺⁰	−1.40×10⁻¹⁵
3.831×10⁻⁰⁴	0.0000000000000000×10⁻¹²	3.8311868495572933×10⁻¹²	3.8311868495572876991119860×10⁻¹²	−1.00×10⁺⁰	+1.47×10⁻¹⁵
1.778×10⁻⁰⁴	0.0000000000000000×10⁻¹²	1.7782794100389226×10⁻¹²	1.7782794100389228012254214×10⁻¹²	−1.00×10⁺⁰	−9.13×10⁻¹⁷
8.254×10⁻⁰⁵	0.0000000000000000×10⁻¹³	8.2540418526801739×10⁻¹³	8.2540418526801842567962891×10⁻¹³	−1.00×10⁺⁰	−1.25×10⁻¹⁵

Observations for the data above: Let \(z = \frac{a^2 + b^2 - c^2}{2ab}\), which is the argument to the arccosine function. The naive algorithm has less relative error when \(z < 1 - 10^{-8}\), because the stable algorithm truncates the cosine series. But for \(z\) above this (i.e. very close to 1), the stable algorithm is more accurate. Moreover, the naive algorithm completely falls apart when \(z > 1 - 10^{-16.5}\), always giving a result of 0 instead of a tiny positive number because the argument \(z\) is closer to 1 than the machine epsilon of double precision.