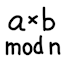Project Nayuki

Montgomery reduction algorithm

Montgomery reduction is a technique to speed up back-to-back modular multiplications by transforming the numbers into a special form. Here I will explain how the algorithm works in precise detail, give mathematical justifications, and provide working code as a demonstration.

For a single multiplication, Montgomery is inferior to doing the modular multiplication directly. But for a chain of multiplications, such as in modular exponentiation, we transform the input numbers into Montgomery form, perform numerous multiplications, and transform back to standard numbers at the end.

Summary

Steps to compute \(c = (a b \text{ mod } n)\):

  1. Choose \(r ∈ \mathbb{N}\) such that \(r > n\) and \(\text{gcd}(r, n) = 1\).

  2. \(k = \frac{r (r^{-1} \text{ mod } n) \, - \, 1}{n}\).

  3. \(\bar{a} = (a r \text{ mod } n)\).
    \(\bar{b} = (b r \text{ mod } n)\).

  4. \(x = \bar{a} \bar{b}\).

  5. \(s = (x k \text{ mod } r)\).

  6. \(t = x + s n\).

  7. \(u = \frac{t}{r}\).

  8. \(\bar{c} = \text{if } (u < n) \text{ then } (u) \text{ else } (u - n)\).

  9. \(c = (\bar{c} r^{-1} \text{ mod } n)\).

Detailed algorithm

Initialization

  1. Problem: We want to compute many instances of \(c ≡ a × b\text{ mod }n\). We will compute with many values of \(a\) and \(b\) but keep \(n\) fixed.

  2. Choose an \(r\) that is greater than \(n\) and coprime with \(n\). Typically we let \(r\) be a power of 2, which means \(n\) needs to be odd and greater than 3.

    Later in the algorithm, we will perform modulo by \(r\) and division by \(r\). With \(r\) being a power of 2, these operations respectively become inexpensive bit masking and right shifting.

    If the base is 10 due to performing decimal arithmetic by hand or using BCD, then \(r\) should accordingly be a power of 10. The reasoning behind the algorithm is still all valid.

  3. Let \(k = \frac{r (r^{-1} \text{ mod } n) \, - \, 1}{n}\). (This division is exact.)

    The reciprocal \(r^{-1} \text{ mod } n\) exists because \(r\) is coprime with \(n\). We know that \(r \, r^{-1} ≡ 1 \text{ mod } n\). Thus \(r \, r^{-1} = 1 + k n\) for some non-negative integer \(k\).

    \(r^{-1} \text{ mod } n\) is computed by the extended Euclidean algorithm.

Outer algorithm

  1. Since we are doing arithmetic modulo \(n\), we assume that all input and output numbers are in the range \([0, n)\). Intermediate results in the algorithm may be larger but not negative.

    In this discussion, we carefully distinguish between equations on integers (\(x = y\)) versus congruences of integers modulo a number (\(x ≡ y \text{ mod } n\)). We also distinguish the use of \(\text{mod}\) as an arithmetic operator versus its use in congruence relations.

  2. First convert the input numbers to Montgomery form: \(\bar{a} = (a r \text{ mod } n)\), \(\bar{b} = (b r \text{ mod } n)\).

    Assume that our desired output in Montgomery form is \(\bar{c} = (c r \text{ mod } n) = (a b r \text{ mod } n)\).

  3. Compute the product directly, so we have: \(\bar{a} × \bar{b} ≡ (a r) (b r) ≡ a b r^2 ≡ \bar{c} r \text{ mod } n\).

    Note that \(0 ≤ \bar{a} × \bar{b} < n^2\).

  4. Now compute the reduction: \(\bar{c} = R(\bar{a} × \bar{b}) = (a b r \text{ mod } n)\).

  5. Finally convert the output back to standard form: \(c = (\bar{c} \, r^{-1} \text{ mod } n)\).

Reduction function

  1. The reduction function \(R : [0, n^2) → [0, n)\) effectively computes \(R(x) = (x \, r^{-1} \text{ mod } n)\) in an efficient way.

  2. Let \(s = (x k \text{ mod } r)\). (\(k\) is defined in the initialization.)

    We know that \(0 ≤ s < r\). By the properties of modular arithmetic, we can replace \(x\) in this expression with \((x \text{ mod } r)\) to get the same result more efficiently.

  3. Let \(t = x + s n\).

    We know that \(0 ≤ x < n^2 < r n\) and \(0 ≤ s n < r n\), thus \(0 ≤ t < 2 r n\). (Recall that we chose \(r > n\).)

    We claim that \(t\) is a multiple of \(r\), with proof:
    \(x + s n \: ≡ \: x + x k n \: ≡ \: x (1 + k n) \: ≡ \: x \, (r \, r^{-1}) \: ≡ \: 0 \: \text{ mod } r\).
    Therefore we can write \(t = u r\) for some non-negative integer \(u\).

    We know that \(t ≡ x \text{ mod } n\) because adding \(s n\) preserves the congruence.

  4. Let \(u = \frac{t}{r}\). (This division is exact.)

    We can see that \(u \: ≡ \: u × 1 \: ≡ \: u \, (r \, r^{-1}) \: ≡ \: (u r) r^{-1} \: ≡ \: t \, r^{-1} \: \text{ mod } n\).

    Moreover, \(u ≡ x \, r^{-1} \text{ mod } n\).

  5. If \(0 ≤ u < n\) then return \(u\). Otherwise return \(u - n\).

    Because \(0 ≤ t < 2 r n\), we have \(0 ≤ u < 2 n\). Hence this simple if-else performs a modulo by \(n\) correctly. Furthermore, the result is still equal (and congruent) to \(x \, r^{-1} \text{ mod } n\).

This completes the explanation and proof of the Montgomery reduction algorithm.

Source code

My runnable implementations of Montgomery reduction for modular multiplication and exponentiation:

More info