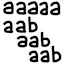Knuth–Morris–Pratt string matching
Introduction
To search for a pattern of length m in a text string of length n, the naive algorithm can take Ɵ(mn) operations in the worst case. For example:
Pattern = aaab Text = aaaaaaaaab Execution: aaaaaaaaab aaab Text offset 0, mismatch at pattern index 3 aaab Text offset 1, mismatch at pattern index 3 aaab Text offset 2, mismatch at pattern index 3 aaab Text offset 3, mismatch at pattern index 3 aaab Text offset 4, mismatch at pattern index 3 aaab Text offset 5, mismatch at pattern index 3 aaab Text offset 6, matched
The Knuth–Morris–Pratt (KMP) string matching algorithm can perform the search in Ɵ(m + n) operations, which is a significant improvement in the worst-case behavior from quadratic time to linear time.
Algorithm
The key observation in the KMP algorithm is this: If currently we already matched the first k characters of the pattern (with 2 ≤ k < m) but the next character in the text mismatches the next character in the pattern, we don’t necessarily need to restart the match from the beginning of the pattern.
For example, if the pattern is abcabd and we partially matched abcab, if the next character isn’t d then we can shorten the partial match to ab (which is both a prefix and a suffix of abcab) instead of restarting from scratch.
Let s be the currently matched k-character prefix of the pattern. If t is some proper suffix of s that is also a prefix of s, then we already have a partial match for t. Compute the longest proper suffix t with this property, and now re-examine whether the next character in the text matches the character in the pattern that comes after the prefix t. If yes, we advance the pattern index and the text index. If no, we repeat this suffix/prefix process until the prefix is empty and we still fail to match the next character.
Let’s associate a number with each character in the pattern: If we matched the prefix s of the pattern up to and including the character at index i, what is the length of the longest proper suffix t of s such that t is also a prefix of s? We will call this the “longest suffix-prefix” (LSP) table. Note that with 0-based indexing, we have 0 ≤ LSP[i] ≤ i for each i.
Examples:
Pattern: a a a a a LSP : 0 1 2 3 4 Pattern: a b a b a b LSP : 0 0 1 2 3 4 Pattern: a b a c a b a b LSP : 0 0 1 0 1 2 3 2 Pattern: a a a b a a a a a b LSP : 0 1 2 0 1 2 3 3 3 4
Now the search algorithm looks like this (Java):
int search(String pattern, String text) {
int[] lsp = computeLspTable(pattern);
int j = 0; // Number of chars matched in pattern
for (int i = 0; i < text.length(); i++) {
while (j > 0 && text.charAt(i) != pattern.charAt(j)) {
// Fall back in the pattern
j = lsp[j - 1]; // Strictly decreasing
}
if (text.charAt(i) == pattern.charAt(j)) {
// Next char matched, increment position
j++;
if (j == pattern.length())
return i - (j - 1);
}
}
return -1; // Not found
}
How do we compute the LSP table? It can be done incrementally with an algorithm very similar to the search algorithm. At each iteration of the outer loop, all the values of lsp before index i need to be correctly computed.
int[] computeLspTable(String pattern) {
int[] lsp = new int[pattern.length()];
lsp[0] = 0; // Base case
for (int i = 1; i < pattern.length(); i++) {
// Start by assuming we're extending the previous LSP
int j = lsp[i - 1];
while (j > 0 && pattern.charAt(i) != pattern.charAt(j))
j = lsp[j - 1];
if (pattern.charAt(i) == pattern.charAt(j))
j++;
lsp[i] = j;
}
return lsp;
}
Source code 
- Java: KmpStringMatcher.java (library), KmpStringMatcherTest.java (JUnit)
- JavaScript: kmp-string-matcher.js
- TypeScript: kmp-string-matcher.ts
- Python: kmpstringmatcher.py
- C: kmp-string-matcher.c
- C++: KmpStringMatcher.cpp
- C#: KmpStringMatcher.cs
- Rust: kmp-string-matcher.rs
License: MIT (open source)
Notes
-
Computing the LSP table is independent of the text string to search. So if the same pattern is used on multiple texts, the table can be precomputed and reused. The KMP algorithm always requires Ɵ(m) extra space for the LSP table.
If precomputation is performed, then preprocessing the pattern takes Ɵ(m) time and searching the text takes worst-case Ɵ(n) time (instead of the combined Ɵ(m + n) time stated at the beginning of the article).
The text string can be streamed in because the KMP algorithm does not backtrack in the text. (This is another improvement over the naive algorithm, which doesn’t naturally support streaming.) If streaming, the amortized time to process an incoming character is Ɵ(1) but the worst-case time is Ɵ(min(m, n′)), where n′ is the number of text characters seen so far.