Project Nayuki

Karatsuba multiplication

Multiplying two \(n\)-bit integers with the naive algorithm takes \(Θ(n^2)\) time. But it can be done faster – with the Karatsuba algorithm it takes \(Θ(n^{\log_2 3}) \approx Θ(n^{1.58})\) time, which gives a significant speed-up for large numbers.

The Karatsuba multiplication algorithm for integers \(x\) and \(y\) is based on the following observations:

  1. Select a modulus \(m ∈ \mathbb{N}^+\). Any number would work, but it’s most efficient to choose a power of 2 that is near \(\sqrt{x}\). This lets the modulo and divide be realized as bit masking and right shifting, and ensures the split is as balanced as possible.

  2. Let \(x_\text{low} = x \text{ mod } m\), and \(x_\text{high} = \lfloor x / m \rfloor\). We have \(x = m x_\text{high} + x_\text{low}\).

  3. Let \(y_\text{low} = y \text{ mod } m\), and \(y_\text{high} = \lfloor y / m \rfloor\). We have \(y = m y_\text{high} + y_\text{low}\).

  4. Let \(a = x_\text{high} y_\text{high}\).

  5. Let \(b = (x_\text{low} + x_\text{high})(y_\text{low} + y_\text{high})\).

  6. Let \(c = x_\text{low} y_\text{low}\).

  7. Then \(xy = am^2 + (b - a - c)m + c\).

Note that in steps 4 through 6, we perform Karatsuba multiplication recursively as long as the numbers are above a certain size.

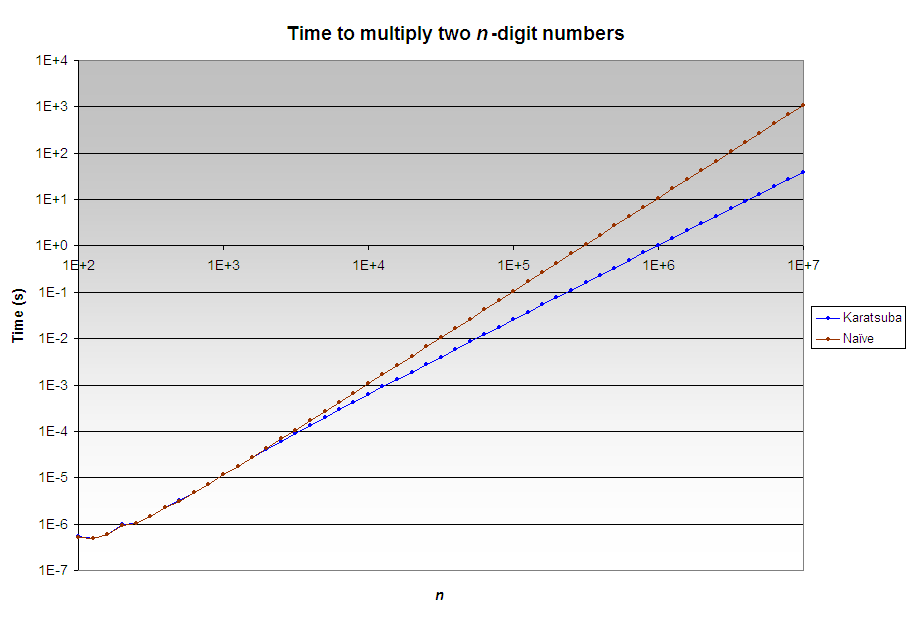
Benchmark

Benchmark graph

The time to multiply two n-bit integers with naive multiplication versus Karatsuba multiplication was measured and graphed. For example, for n = 107 bits, naive multiplication took 1079 seconds while Karatsuba multiplication took 39 seconds, implying a 28× speed-up. Karatsuba multiplication starts to be faster than naive multiplication at around n = 3000 bits.

The tests were performed on Intel Core 2 Quad Q6600 (2.40 GHz) using a single thread, Windows XP SP 3, Java 1.6.0_22.

Older versions of Java (SE 7 and below) used the \(Θ(n^2)\) naive algorithm for BigInteger.multiply(), so the code offered on this page would achieve an improvement in speed. But Java SE 8 introduced an implementation of Karatsuba multiplication and Toom–Cook multiplication, and uses these faster algorithms appropriately when operating on longer numbers. So the benchmark results on this page are only valid for Java SE 7 and below. To perform benchmarking on Java SE 8 and above, you would need to manually reimplement the naive multiplication or copy the Java standard library’s implementation while stripping out the faster algorithms.

Source code

More info