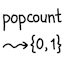Project Nayuki

Iterated popcount results in 0 or 1

Theorem

By repeatedly applying the popcount function to any positive integer, the result will eventually be 1 and stay that way.

More formally: For each integer \(n ≥ 1\), there exists \(k ≥ 0\) such that \(\text{popcount}^{(k)}(n) = 1\).

Proof

(A highly abridged proof for busy, seasoned mathematicians: \(1 ≤ \text{popcount}(n) < n\) for all \(n ≥ 2\). By well-ordering, iterating \(\text{popcount}\) will eventually produce \(1\).)

Definition: The popcount function, also known as Hamming weight, is the number of 1’s in the binary representation of a non-negative integer. For example, \(\text{popcount}(13) = \text{popcount}(1101_2) = 3\).

By inspection, 0 and 1 are fixed points of this function – namely, \(\text{popcount}(0) = 0\) and \(\text{popcount}(1) = 1\). This means whenever \(\text{popcount}(n) = 1\), we know that \(\text{popcount}(\text{popcount}(n)) = 1\). So once the iteration process reaches \(1\), it keeps producing \(1\) identically.

Lemma alpha

Whenever \(n ≥ 4\), \(n\) is greater than the number of binary digits \(n\) has. More formally: \(\forall n ∈ \mathbb{N}, \: (n ≥ 4 \: ⇒ \: n > \left\lfloor \log_2 n \right\rfloor + 1)\).

Intuitively speaking, this is true because the number of bits is a non-decreasing function that increases by merely 1 every time its input doubles. At 4, the function value is 3; at 8 the function value is 4; at 16 the function value is 5. The function value always grows more slowly than the input value. A proof by strong induction will be omitted.

Lemma beta

For \(n ≥ 2\), we can show that \(1 ≤ \text{popcount}(n) < n\).

By definition, \(\text{popcount}(n)\) is no more than the number of binary digits in \(n\). We also know that each positive integer must have at least one bit set to 1. Hence for \(n ≥ 1\), we have \(1 ≤ \text{popcount}(n) ≤ \left\lfloor \log_2 n \right\rfloor + 1\).

For the cases of \(n = 2, 3\), we can compute that \(\text{popcount}(2) = 1 < 2\) and \(\text{popcount}(3) = 2 < 3\).

For the case of \(n ≥ 4\), combining the above inequality and lemma alpha implies \(1 ≤ \text{popcount}(n) ≤ \left\lfloor \log_2 n \right\rfloor + 1 < n\) as wanted.

Lemma gamma

For each \(n ≥ 1\), the set of all values from iterating \(\text{popcount}\) on \(n\) contains the value \(1\).

Formally speaking, \(\forall n ∈ \mathbb{N}^+, \: 1 ∈ \{\text{popcount}^{(k)}(n) \: | \: k ∈ \mathbb{N} \}\).

Call this set as \(S\), which we know is a subset of the natural numbers. We know that the set is non-empty because it contains \(n\) when \(k = 0\). By the well-ordering of natural numbers, \(S\) must have a minimal element \(m\).

If \(m\) is at least \(2\), then this cannot happen because by lemma beta, \(\text{popcount}(m) < m\) but \(\text{popcount}(m) ∈ S\). \(m\) also is not \(0\) because the \(\text{popcount}\) of a positive integer is positive. So the minimal element must be \(1\), thus \(1\) is in \(S\).

Therefore by the definition of \(S\), there must exist some \(k ∈ \mathbb{N}\) such that \(\text{popcount}^{(k)}(n) = 1\).

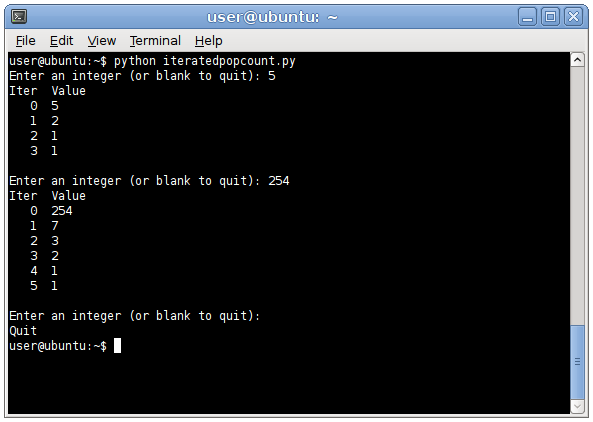
Demonstration

Program demo screenshot

Notes

  • Iterating popcount on a CPU register can achieve the same result as computing the C expression n == 0 ? 0 : 1, which coerces all non-zero values to 1. For a 64-bit register, this computation can be implemented with 4 iterations of popcount to work correctly on all 64-bit integer values. This can be useful for cryptography for example, as it is one of the many possible ways to compute the integer-to-Boolean coercion in constant time to prevent timing analysis attacks.

  • If \(n\) is the smallest integer that requires \(k\) iterations of \(\text{popcount}\) to reach \(1\), then \(2^n - 1\) is the smallest integer that requires \(k + 1\) iterations. For example, \(7\) requires \(3\) iterations, \(127\) requires \(4\) iterations, and \(2^{127} - 1\) requires \(5\) iterations.

  • A number that requires 6 iterations of popcount to reach 1 will never fit on a computer in binary form, because it’ll require 2127 bits, or equivalently 21 trillion yottabytes. (But it is possible to describe these large numbers in exponential notation or in algebraic form.) So it’s safe to say that 5 iterations of popcount will bring any non-negative integer to either 0 or 1 on any real-world computer.

  • The proof presented on this page can be applied to other natural number functions as well, such as the number of divisors a number has and the totient function. The heart of the argument is that the function’s output is smaller than its input for almost all natural numbers, hence well-ordering guarantees that the iteration process will eventually reach a fixed point.