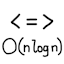Is there an ideal comparison sort?
Every computer science student should have studied or at least encountered sorting algorithms early in their career. There are many well-known sorting algorithms, including bubble sort, selection sort, insertion sort, Shell short, heapsort, merge sort, quicksort, and radix sort. Each one has different characteristics and tradeoffs. An open question I would like to ask is, is there a comparison sorting algorithm that has all the ideal properties?
- Comparison sort
A comparison sort only extracts information from the list’s elements by comparing two of them at a time. Comparing \(x\) and \(y\) gives exactly one of three results: \(x < y\), \(x = y\), or \(x > y\). A comparison sort does not extract any other information, such as the size of an element or the bit representation of it. This rules out algorithms like radix sort. It is known that a comparison sort on a list of \(n\) elements (performed on a serial machine) must have worst-case time complexity \(Ω(n \log n)\).
- Worst-case time complexity
The naive sorting algorithms, like bubble sort and insertion sort, have time complexity \(Θ(n^2)\). The best comparison sorting algorithms have time complexity \(Θ(n \log n)\). However, quicksort has random-case time complexity \(Θ(n \log n)\) but worst-case time complexity \(Θ(n^2)\).
- Worst-case auxiliary space complexity
Some sorting algorithms operate in-place, using \(Θ(1)\) extra (auxiliary) space. Some need lots of extra space, as much as \(Θ(n)\). Ideally, a sorting algorithm should only use \(O(1)\) extra space.
- Stability
Elements are being sorted by their keys, but the elements may hold extra data that is not considered in sorting. A stable sorting algorithm keeps the relative order of elements that have the same key. This is useful for sorting the same list by one key followed by sorting by another key. Any unstable sorting algorithm can be modified to be stable by using \(O(n)\) extra space.
Here are the characteristics of popular sorting algorithms:
| Algorithm | Comparison sort | Worst-case time | Worst-case extra space | Stable |
|---|---|---|---|---|
| Bubble sort | Yes | \(Θ(n^2)\) | \(Θ(1)\) | Yes |
| Selection sort | Yes | \(Θ(n^2)\) | \(Θ(1)\) | No |
| Insertion sort | Yes | \(Θ(n^2)\) | \(Θ(1)\) | Yes |
| Shellsort | Yes | Between \(Θ(n \log n)\) and \(Θ(n^2)\) | \(Θ(1)\) | No |
| Heapsort | Yes | \(Θ(n \log n)\) | \(Θ(1)\) | No |
| Merge sort | Yes | \(Θ(n \log n)\) | \(Θ(n)\) | Yes |
| Quicksort | Yes | \(Θ(n^2)\) | \(Θ(\log n)\) | No |
| Radix sort | No | \(Θ(nk)\), where \(k\) is the number of bits | \(Θ(n)\) | Yes |
So my question is, is there a comparison sorting algorithm that has worst-case time complexity \(Θ(n \log n)\), worst-case auxiliary space complexity \(Θ(1)\) (or perhaps up to \(O(\log n)\)), and is stable?
I have come across mentions of an in-place stable merge sort algorithm, but was unable to find a description that I could understand. Examples include [0], [1], [2], [3], [4], [5], [6], [7].