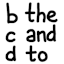 Huffman-coding English words
Huffman-coding English words
Introduction
We know that some letters occur more frequently than others in English text. E and T are the two most common letters. A typical homework exercise for computer science students is to write a program that creates an optimal Huffman code for the English alphabet, and try to encode some texts with it to observe the compression achieved.
Let’s take it a step further and consider English words instead of individual letters. In a typical block of text, some words – like the, and, is – occur far more often than others. What would happen if we replaced common words with short letter sequences and uncommon words with longer sequences – what would the result look like? Consider this as an experiment in increasing the information entropy of natural language text...
Sample text
For these encoding experiments, the full text of the book Alice’s Adventures in Wonderland by Lewis Carroll was used. The text was preprocessed to remove the hard line wrapping newlines within paragraphs because the encoding schemes described here will change the word lengths and thus the line lengths. When you view the full text files, you will need a text editor that supports soft line wrapping.
Full text files:
- Original text (from Project Gutenberg)
- Input text (164 KB) (line breaks removed)
- Sort coding output (119 KB)
- Huffman coding output (109 KB)
Paragraph samples: (Tip: hover over an encoded word to see the original word)
| Original | Sort coding | Huffman coding |
|---|---|---|
| CHAPTER IV. The Rabbit Sends in a Little Bill | MX aIV. B Ec aSends l e Bk Je | TzvHR. AhEhBAFKWAHdRCMIPPVF QJ |
| 'Hand it over here,' said the Dodo. | 'Ie g fa eb,' k b Ma. | 'CTNKEshEPGI,' cDAND. |
| Alice was beginning to get very tired of sitting by her sister on the bank, and of having nothing to do: once or twice she had peeped into the book her sister was reading, but it had no pictures or conversations in it, 'and what is the use of a book,' thought Alice 'without pictures or conversations?' | M n ke d em bg wr f pv ci q rg v b bkt, c f pg fo d bt: fp bd bdd h z bqz cv b nq q rg n bii, ba g z bs bhx bd bxt l g, 'c bh bi b ga f e nq,' cm M 'fq bhx bd bxt?' | xlTFOCXAdgaUXkBUAGqbAXDAUT, JUZAGuOGk: HEAZqN YAJAQVBaDAERAGqblLFNWIKi, AchAJBTACFAZAwW dAK, 'JBIBGDGAURji,' Bex'EGACFAZAwW?' |
| Alice was not a bit hurt, and she jumped up on to her feet in a moment: she looked up, but it was all dark overhead; before her was another long passage, and the White Rabbit was still in sight, hurrying down it. There was not a moment to be lost: away went Alice like the wind, and was just in time to hear it say, as it turned a corner, 'Oh my ears and whiskers, how late it's getting!' She was close behind it when she turned the corner, but the Rabbit was no longer to be seen: she found herself in a long, low hall, which was lit up by a row of lamps hanging from the roof. | M n bc e jo bop, c h xx bo v d q ip l e fy: h eo bo, ba g n w bmb aoverhead; ex q n hq fs bht, c b Gh Ec n mo l pu, ahurrying bq g. Br n bc e fy d bb bpo: gp cf M cb b cmc, c n du l cr d kl g ed, p g ka e bes, 'Ep dh bap c buf, cq xy g't hs!' H n lx lv g ch h ka b bes, ba b Ec n bs bpn d bb ks: h fl ce l e fs, ko qo, dn n alit bo ci e chk f alamps boh ea b yq. | xlAeRgEpfLP, JYrNBKAXOAGXQdRXv: YCOHr, AchlAMATWSAjFLpFNW; HHAGlHAEVACJ, JDGmEhlTXdaQ, pfLLAAIKi BRAK. EtlAeRGvOAYART: HjBPxBSDAmN, JlCQdCKOQQhHv, shHsRADz, 'jxBpADlJANT, CVARiAK'AHiFPPIKi!' EAlTnTohBVYHsDADz, AcDEhlBTAsOOAYAPn: YELCedRAsQ, gzZp, CJlVIAFBKBURApgUVNtkAHASGCSDLSSAI. |
Codebook sample for sort coding:
a ESC b the c and d to e a f of g it h she i i j you k said l in m alice n was o that ... fw tell fx hare fy moment fz put ga use gb d ... cmi wretched cmj yawned cmk yawning cml year cmm years
Codebook sample for Huffman coding:
AA “y” ABA “too” ABB “tongue” ABC “tm” ABD “tiny ” ... AF “t ” AG “her ” AH “s ” AI “f” AJ “had ” AK “it” AL “Alice” AM “all ” ... Azx “Knave” Azy “Keep ” Azz “J” BA “S” BB “out ” BC “he ” BDA “Its ” BDB “IT ” BDC “IT” BDD “Hush” BDE “Hart” ... BI “what ” BJ “you” BK “up ” BL “Project ” BM “were ” BN “if ” BO “one ” BP “went ” BQ “have ” BR “down ” BS “like ” BT “no ” ... I “i” J “and ” K “n” L “r” M “s” N “a” O “to ” P “t” ... uy “tree ” uz “tree” v “I” w “that ” x “Alice ” y “at ” z “with ”
Algorithms
First, let’s clarify how the input text is interpreted. We assume that it is in plain text format (no markup, HTML, etc.). We define the input text to be a sequence of tokens, where each token is either a single symbol (such as space, punctuation, number, newline) or a word (a sequence of consecutive uppercase/lowercase letters). We also disallow two-word tokens being adjacent (e.g. we can’t treat tome as the two consecutive words to me with no symbols in between).
Sort coding
We start by illustrating a simpler algorithm before considering Huffman coding. If we encode each input word into some other word, then word boundaries are preserved by the symbols and each encoded word is still easily decodable. In particular, we don’t need to make use of the prefix decodability property of Huffman codes.
Therefore, we can devise a simple coding scheme based on sorting:
Count the number of occurrences of each word in the text.
Assign a codeword to each unique word, starting with the most frequent word and working downward in frequency. The most frequent word is given the codeword a, the next word is given b, next c, ..., z, aa, ab, ..., az, ba, bb, ..., zz, baa, etc.
Write the word-codeword mapping to the output. (Otherwise decoding is impossible.)
Iterate through the input tokens, mapping word tokens to their codeword and leaving symbol tokens unchanged, and write the token strings to the output file.
However, there are a few additional details I chose to implement:
-
The input word case is mapped analogously to the output codeword case. For example, suppose the codeword for food (lowercase) is nb. Then Food (title case) is Nb and FOOD (uppercase) is NB.
If a word/codeword is a single uppercase letter, then we consider it to be title case instead of uppercase, because title case words are more common than fully uppercase ones. However, a problem is that if the codeword is a single letter, we can only encode lowercase and title case but not uppercase. Also, WeIrD caSE Words can’t have their letter case encoded into the codeword because most codewords are shorter than the original word. So we need an escape mechanism for these situations.
Because of this, when we count word frequencies we consider the lowercase, title case, and uppercase versions of a word to be the same word. In other words, frequency-counting is case-insensitive (except we skip weird case words).
Some words appear in the text only once (hapax legomena). Because we need to transmit a dictionary of word-codeword mappings to the decoder, it’s not worth the space to map these single-use words. Once again, we need an escape mechanism.
The escape mechanism is that if the codeword begins with a, then the rest of the letters in the codeword is the literal word to be encoded. The letter cases are preserved. This means no other codeword can begin with a, so we actually need to start normal codewords with b to z (the subsequent letters can be a though). (Note that this also means the prefix A is wasted.)
Huffman coding
Now we come to Huffman coding, the main part of the experiment. We first observe that sort coding is essentially optimal; we need to change the operational model before Huffman coding becomes useful. In particular, we want to take advantage of the prefix-free property – in a Huffman-coded text, we don’t need spaces between words because the codewords are self-delimiting!
Therefore, let’s consider a word followed by a space to be a single word for the purposes of encoding. This is the most common word+symbol combination; others like word+comma or word+apostrophe exist but we’ll disregard them for simplicity. Note that word+space is a different word than just the word itself. For example, assume the codebook is {“the” = xa, “the ” = k, “quick” = oql}. Then we can encode the text “the quick” as either xa oql (the space quick) or koql (the+space quick).
The encoding procedure looks like this:
Count the number of occurrences of each word in the text. We consider a word followed by space to be a single word.
Construct a Huffman code tree for the set of words and frequencies.
Write the word-codeword mapping to the output. (Otherwise decoding is impossible.)
Encode the input text tokens into tokens for the output text. Note that some of the space tokens in the input will collapse into the preceding word.
Note that symbols other than space are not Huffman-coded at all. This is a deliberate design so that the output text looks readable and can be meaningful compared to the input text.
Again, I chose to make some modifications to the basic algorithm to improve the efficiency of the coding, at a cost to complexity:
If a trailing-space word has a frequency of 1, then merge its frequency with the non-space version of the word. (This means when we encounter this word plus the space, we will encode the word and the space separately.)
If a word has a frequency of 1, then delete the word and start accumulating the frequencies of its constituent letters.
The input words and output codewords are treated as case-sensitive. Thus lowercase and uppercase words are considered completely distinct.
Source code 
- SortTextEncoder.java
- SortTextDecoder.java
- HuffmanTextEncoder.java
- HuffmanTextDecoder.java
- TextTokenizer.java
Notes
The encoder-decoder pairs are designed to be lossless (except for bugs). Thus all the nuances of the input text, such as line breaks and double spaces and weird symbols, will be properly preserved in the decoded output.
The dictionary-based coding schemes implemented here are reminiscent of Lempel–Ziv compression algorithms like LZ78 and LZW. These are the serious compression schemes we’d use in real life. But they defy the rules of English, like grabbing “words” that begin in the middle of a word, and include multiple punctuation marks and parts of another word.
The entire Alice in Wonderland text file has about 3000 unique words, and the main Alice text (sans the Project Gutenberg header/footer) has about 2500 unique words. This actually doesn’t stress-test the Huffman coding mechanism enough; we see that both sort coding and Huffman coding max out at mere 3-letter codewords.
One suboptimal property of the Huffman coding implemented here is that all codewords have the prefix-free property, even though it’s unnecessary in the situation where a symbol follows a codeword. For example, if b and bk are both codewords, then bkop might have an ambiguous decoding, but b! and bk! are both unambiguous because the symbol terminates the decoding. Also, doing 52-ary Huffman coding is wildly inefficient compared to the already inefficient binary Huffman coding; serious compression applications always use a form of arithmetic coding instead of whole-bit coding. Additionally, the logic for skipping hapax legomena and breaking up words into characters are heuristics, not provably optimal.