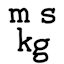 Handling physical quantities in math formulas
Handling physical quantities in math formulas
Introduction
In math class and especially science class (physics, chemistry, etc.), you do calculations that have physical quantities as inputs and yield a physical quantity as an answer. For example, a rectangle that is 3 metres wide and 2 metres long has an area of 3 × 2 = 6 square metres.
Many teachers gloss over how to handle measurement units properly in math formulas. They simply expect you to plug in the numbers, calculate the numerical result, and tack on the expected unit at the end (such as \(\text{m}^2\)). But this shortcut method of working with units is misleading at best and dangerous at worst. Because the units don’t participate in the calculation and are added on as an afterthought, it’s harder to detect calculation errors from the use of mismatched units, and it’s possible to use the wrong formula without noticing (such as using a volume formula instead of an area formula).
Actually, it’s practical to handle physical quantities/units in a rigorous way, and in this article I will explain and illustrate how. You only need to know basic algebra to understand the main concept of working with units. Also, all physical units (such as metre, second, gram, etc.) will be treated as opaque, positive variables that follow all the rules of algebra.
Unit conversions
In this world, there are many ways to measure the same kind of quantity. For example, length can be measured in metres (symbol: m) or feet (symbol: ft). Because these units measure the same kind of thing, they can be equated with a conversion factor.
For example, 1 foot is exactly 0.3048 metres. We can write this as an equation: \(1\text{ ft} = 0.3048\text{ m}\).
We can take the equation and rearrange it to get this: \(\frac{1\text{ ft}}{0.3048\text{ m}} = 1\).
It might look unusual but it will be useful in a moment.
Similarly, we can rearrange in a different way to get: \(\frac{0.3048\text{ m}}{1\text{ ft}} = 1\).
As another example, \(1000\text{ m} = 1\text{ km}\), hence \(\frac{1000\text{ m}}{1\text{ km}} = 1 = \frac{1\text{ km}}{1000\text{ m}}\).
Armed with these fractions equaling one, we multiply by any of them to perform unit conversions.
For example, what is 3125 feet in kilometres? Let’s do the algebra:
\(\require{cancel} 3125\text{ ft} \:=\: 3125\text{ ft} × 1 × 1 \:=\: 3125\text{ ft} ×\! \frac{0.3048\text{ m}}{1\text{ ft}} \!×\! \frac{1\text{ km}}{1000\text{ m}} \:=\: \frac{3125 \,×\, 0.3048 \,×\, 1\, \cancel{\text{ft}} \cdot \cancel{\text{m}} \cdot\, \text{km}}{1 \,×\, 1000\, \cancel{\text{ft}} \cdot \cancel{\text{m}}} \:=\: 0.9525\text{ km}\).
Formulas
We know that the area of a rectangle is \(A = l × w\), where \(l\) is the length and \(w\) is the width. Let’s look at some examples of applying the formula:
- Rectangle with \(l = 50\text{ cm}, w = 20\text{ cm}\):
-
Thus \(A \:=\: (50\text{ cm})(20\text{ cm}) \:=\: 1000 \: (\text{cm})^2 \:=\: 1000 \text{ cm}^2\).
This is the easy case, which is when all the units agree with each other. Most textbooks don’t exceed this level of difficulty.
- Rectangle with \(l = 74\text{ m}, w = 81\text{ km}\):
-
Thus \(A = (74\text{ m})(81\text{ km}) = 5994\text{ m} \cdot \text{km} = 5994\text{ m} \cdot \text{km} × \frac{1\text{ km}}{1000\text{ m}} = \frac{5994\, \cancel{\text{m}} \cdot\, \text{km} \,\cdot\, \text{km}}{1000\, \cancel{\text{m}}} = 5.994 \text{ km}^2\).
Here we got an intermediate result that is expressed in metres-times-kilometres (which is a measure of area). It’s technically correct but ugly, so we multiplied by a conversion factor to get an answer in square kilometres.
- Rectangle with \(l = 3\text{ mi}, w = 2\text{ km}\):
-
Thus \(A \:=\: (3\text{ mi})(2\text{ km}) \:=\: 6\text{ mi} \cdot \text{km} \:\approx\: 6\text{ mi} \cdot \text{km} × \frac{1.609\text{ km}}{1\text{ mi}} \:\approx\: 9.654\text{ km}^2\).
The technique of doing algebra with units will work even for complicated formulas with more variables and types of units. For example, Newton’s law of gravitation says that the force of attraction between two bodies is \(F = \frac{G \, m_1 \, m_2}{d^2}\), where \(G \approx (6.67384 × 10^{-11}\text{ m}^3 \cdot \text{kg}^{-1} \cdot \text{s}^{-2})\) is a constant, \(m_1\) is the mass of one object, \(m_2\) is the mass of the other object, and \(d\) is the distance between both objects.
Let’s apply the gravitation formula in an example: \(m_1 = 7000\text{ kg}, m_2 = 4\text{ kg}, d = 0.01\text{ m}\).
Thus \(F \:=\: \frac{6.67384 \,×\, 10^{-11}\text{ m}^3}{\text{kg} \,\cdot\, \text{s}^2} \frac{(7000\text{ kg})(4\text{ kg})}{(0.01\text{ m})^2} \:\approx\: 1.869 × 10^{-2}\text{ m} \cdot \text{kg} \,/\, \text{s}^2 \:\approx\: 1.869 × 10^{-2}\text{ N}\).
Functions
Sometimes a physical quantity is described by a function of one or more variables, which can be evaluated at multiple values. For example, an object in free fall has a height that is a quadratic function of time.
In the lazy way given in textbooks, a scenario would look like this:
A ball fired from a cannon has height \(h(t) = -4.9t^2 + 8t + 3\), where \(t\) is in seconds and \(h(t)\) is in metres.
To evaluate this function at \(t = 2\text{ s}\), you would have to ensure that \(t\) is given in seconds (or converting to satisfy this requirement), then strip off the unit so that you get the dimensionless number of 2, evaluate the formula to get −0.6, and append the unit to get −0.6 metres.
The more correct but cumbersome way would look like this:
A ball fired from a cannon has height \(h(t) = (-4.9(t / \text{s})^2 + 8(t / \text{s}) + 3) \text{ m} = (-4.9 \text{ m} / \text{s}^2) \, t^2 + (8 \text{ m} / \text{s}) \, t + (3 \text{ m})\) at time \(t\).
Notice now that inside the formula there are units, but outside the formula (in the description of the variables) there are no units. We can see that this is the reverse situation of the first example. Also notice that the first term looks like an acceleration due to the unit of \(\text{m} / \text{s}^2\), the second term looks like a constant speed due to the unit of \(\text{m} / \text{s}\), and the last term looks like a constant height offset due to the unit of \(\text{m}\). If we evaluate this function at \(t = 2\text{ s}\), we get exactly the same answer as before, but more rigorously: \(h(t) \:=\: (-4.9 \text{ m} / \text{s}^2)(2\text{ s})^2 + (8 \text{ m} / \text{s})(2\text{ s}) + (3 \text{ m}) \:=\: (-4.9 × 2^2\text{ m}) + (8 × 2\text{ m}) + (3\text{ m}) \:=\: -0.6\text{ m}\).
Calculus
Derivatives and integrals are useful concepts in physics. For example, speed is the derivative of displacement, and area is the integral of line lengths. The good news is that taking the derivative or integral of a function will automatically respect the units.
To illustrate as an example, the previous section described a function that calculates the height of a cannonball when given the time. If we take the derivative of the function, we get: \(\frac{d}{dt} h(t) \:=\: (-4.9 \text{ m}/\text{s}^2)(2t) + (8 \text{ m}/\text{s})(1) + (0) \:=\: (-9.8 \text{ m}/\text{s}^2) \, t + (8\text{ m}/\text{s})\). We expect this to be a formula for speed. Indeed when we plug in a value for \(t\), we get an answer that is expressed in \(\text{m}/\text{s}\).
Error detection
When calculating with explicit units, any mismatched units will show up in the final result. For example:
A rectangle is measured lengthwise in kilometres and widthwise in miles. Then multiplying the two numbers will give an area correctly measured in kilometres-times-miles. If units were not handled during the calculation, it would be a mistake to assume that the answer is given in square kilometres or square miles.
When applying Newton’s gravitation formula with a distance measured in \(\text{km}\) (instead of \(\text{m}\)), the result will have a unit of \(\frac{\text{m}^3 \,\cdot\, \text{kg}}{\text{km}^2 \,\cdot\, \text{s}^2}\) (or equivalently \(\text{N} \cdot \text{m}^2 / \text{km}^2\)) instead of \(\text{m} \cdot \text{kg} / \text{s}^2\) (or just \(\text{N}\)), and you would notice the discrepancy. If you did the calculation without units, it would be easy to not notice the mismatched units because there are 3 variables with various units and one constant with a rather complicated compound unit.
When choosing a formula to use, you can rule out candidates when they give nonsensical units. This method is called dimensional analysis. For example:
If hypothetically \(V = \pi r^2\) were the formula for a sphere’s volume, then having \(r\) in metres would give a so-called volume result in square metres. But volume is actually measured in cubic metres, so this formula must be incorrect for calculating volume.
-
Problems involving electrical quantities tend to be less intuitive and more abstract than mechanics problems. This is because there is one more base unit (ampere) and many more derived units defined (volt, watt, farad, weber, etc.). So it’s easier to accidentally pick the wrong formula when setting up a calculation.
For example, \(\text{Power } (P) = \text{Voltage } (V) × \text{Current } (I)\) is a valid way to calculate power. But \(P = V × \text{Resistance } (R)\) is invalid. However \(P = V^2 \,/\, R\) is in fact valid.
None of these three formulas are obvious at a glance, so let’s verify them. First, some important unit definitions:
- Unit of force – newton: \(\text{N} = \frac{\text{kg} \,\cdot\, \text{m}}{\text{s}^2}\).
- Unit of work – joule: \(\text{J} = \text{N} \cdot \text{m} = \frac{\text{kg} \,\cdot\, \text{m}^2}{\text{s}^2}\).
- Unit of power – watt: \(\text{W} = \text{J} \,/\, \text{s} = \frac{\text{kg} \,\cdot\, \text{m}^2}{\text{s}^3}\).
- Unit of electric potential – volt: \(\text{V} = \text{J} \,/\, \text{C} = \frac{\text{kg} \,\cdot\, \text{m}^2}{\text{C} \,\cdot\, \text{s}^2}\).
- Unit of electric current – ampere: \(\text{A} = \text{C} \,/\, \text{s} = \frac{\text{C}}{\text{s}}\).
- Unit of electrical resistance – ohm: \(\text{Ω} = \text{V} \,/\, \text{A} = \frac{\text{kg} \,\cdot\, \text{m}^2}{\text{C}^2 \,\cdot\, \text{s}}\).
Now, onto verifying the formulas:
First formula: \(\text{V} × \text{A} = \frac{\text{kg} \,\cdot\, \text{m}^2}{\cancel{\text{C}} \cdot\, \text{s}^2} \frac{\cancel{\text{C}}}{\text{s}} = \frac{\text{kg} \,\cdot\, \text{m}^2}{\text{s}^3} = \text{W}\). Power is measured in watts, which is correct.
Second formula: \(\text{V} × \text{R} = \frac{\text{kg} \,\cdot\, \text{m}^2}{\text{C} \,\cdot\, \text{s}^2} \frac{\text{kg} \,\cdot\, \text{m}^2}{\text{C}^2 \,\cdot\, \text{s}} = \frac{\text{kg}^2 \,\cdot\, \text{m}^4}{\text{C}^3 \,\cdot\, \text{s}^3} \neq \text{W}\). The resulting unit does not measure power.
Third formula: \(\text{V}^2 \,/\, \text{R} = \left( \frac{\text{kg} \,\cdot\, \text{m}^2}{\text{C} \,\cdot\, \text{s}^2} \right)^2 \left( \frac{\text{kg} \,\cdot\, \text{m}^2}{\text{C}^2 \,\cdot\, \text{s}} \right)^{-1} = \frac{\text{kg} \,\cdot \cancel{\text{kg}} \,\cdot\, \text{m}^2 \,\cdot \cancel{\text{m}^2}}{\cancel{\text{C}^2} \cdot\, \text{s}^3 \,\cdot \cancel{\text{s}}} \frac{\cancel{\text{C}^2} \cdot \cancel{\text{s}}}{\cancel{\text{kg}} \cdot \cancel{\text{m}^2}} = \text{W}\). This formula passes the basic test of units.
By doing dimensional analysis, we can discard nonsensical calculations before we waste time trying to apply their results.