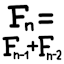Fast Fibonacci algorithms
Introduction
Definition: The Fibonacci sequence is defined as \(F(0) = 0\), \(F(1) = 1\), and \(F(n) = F(n-1) + F(n-2)\) for \(n ≥ 2\). So the sequence (starting with \(F(0)\)) is 0, 1, 1, 2, 3, 5, 8, 13, 21, ….
If we want to compute a single term in the sequence (e.g. \(F(n)\)), there are a couple of algorithms to do so. Some algorithms are much faster than others.
Algorithms
- Textbook recursive (extremely slow)
Naively, we can directly execute the recurrence as given in the mathematical definition of the Fibonacci sequence. Unfortunately, it’s hopelessly slow: It uses \(Θ(n)\) stack space and \(Θ(φ^n)\) arithmetic operations, where \(φ = \frac{\sqrt{5} + 1}{2}\) (the golden ratio). In other words, the number of operations to compute \(F(n)\) is proportional to the final numerical answer, which grows exponentially.
- Dynamic programming (slow)
It should be clear that if we already computed \(F(k-2)\) and \(F(k-1)\), then we can add them to get \(F(k)\). Next, we add \(F(k-1)\) and \(F(k)\) to get \(F(k+1)\). We repeat until we reach \(k = n\). Most people notice this algorithm automatically, especially when computing Fibonacci by hand. This algorithm takes \(Θ(1)\) space and \(Θ(n)\) operations.
- Matrix exponentiation (fast)
-
The algorithm is based on this innocent-looking identity (which can be proven by mathematical induction):
\( \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]^n = \left[ \begin{matrix} F(n+1) & F(n) \\ F(n) & F(n-1) \end{matrix} \right] \).
It is important to use exponentiation by squaring with this algorithm, because otherwise it degenerates into the dynamic programming algorithm. This algorithm takes \(Θ(1)\) space and \(Θ(\log n)\) operations. (Note: We are counting the number of bigint arithmetic operations, not fixed-width word operations.)
- Fast doubling (faster)
-
Given \(F(k)\) and \(F(k+1)\), we can calculate these:
\(\begin{align} F(2k) &= F(k) \left[ 2F(k+1) - F(k) \right]. \\ F(2k+1) &= F(k+1)^2 + F(k)^2. \end{align}\)
These identities can be extracted from the matrix exponentiation algorithm. In a sense, this algorithm is the matrix exponentiation algorithm with the redundant calculations removed. It should be a constant factor faster than matrix exponentiation, but the asymptotic time complexity is still the same.
Summary: The two fast Fibonacci algorithms are matrix exponentiation and fast doubling, each having an asymptotic complexity of \(Θ(\log n)\) bigint arithmetic operations. Both algorithms use multiplication, so they become even faster when Karatsuba multiplication is used. The other two algorithms are slow; they only use addition and no multiplication.
Source code 
Implementations are available in multiple languages:
Java: FastFibonacci.java (all 3 algorithms, timing benchmark, runnable main program)
Python: fastfibonacci.py (fast doubling function only)
JavaScript: fastfibonacci.js (fast doubling function only)
Haskell: fastfibonacci.hs (fast doubling function only)
C#: FastFibonacci.cs (fast doubling only, runnable main program)
(requires .NET Framework 4.0 or above; compile withcsc /r:System.Numerics.dll fastfibonacci.cs)
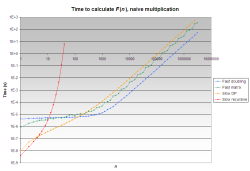
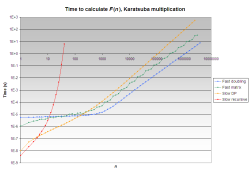
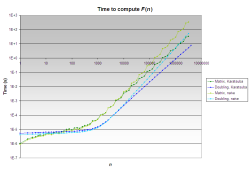
Benchmarks
Graphs
The following graphs show the running time as a function of the input number. Both the x and y axes have logarithmic scales.
All algorithms, naive multiplication
All algorithms, Karatsuba multiplication
Fast algorithms, both multiplication algorithms
Table
The running time (in nanoseconds with 4 significant figures) as a function of the input number:
| n | Fast doubling, Karatsuba multiplication | Fast matrix, Karatsuba multiplication | Fast doubling, naive multiplication | Fast matrix, naive multiplication | Slow dynamic programming | Slow recursive |
|---|---|---|---|---|---|---|
| 1 | 5 414 | 1 042 | 4 197 | 887 | 10 | 4 |
| 2 | 5 638 | 2 092 | 4 442 | 1 822 | 53 | 22 |
| 3 | 5 708 | 2 740 | 4 509 | 2 342 | 92 | 56 |
| 4 | 5 945 | 3 027 | 4 733 | 2 660 | 133 | 114 |
| 5 | 5 989 | 3 677 | 4 787 | 3 147 | 172 | 219 |
| 6 | 5 972 | 3 956 | 4 765 | 3 371 | 211 | 400 |
| 8 | 6 191 | 3 972 | 4 969 | 3 428 | 289 | 1 161 |
| 10 | 6 283 | 4 952 | 5 022 | 4 154 | 370 | 3 113 |
| 13 | 6 307 | 5 610 | 5 046 | 4 667 | 488 | 13 480 |
| 16 | 6 479 | 4 955 | 5 177 | 4 210 | 605 | 57 300 |
| 20 | 6 542 | 5 923 | 5 234 | 4 985 | 763 | 394 000 |
| 25 | 6 632 | 6 565 | 5 263 | 5 479 | 964 | 4 373 000 |
| 32 | 6 794 | 5 887 | 5 388 | 4 908 | 1 235 | 127 500 000 |
| 40 | 6 818 | 6 880 | 5 433 | 5 715 | 1 552 | 5 980 000 000 |
| 50 | 6 806 | 7 742 | 5 486 | 6 446 | 2 023 | |
| 63 | 6 931 | 10 180 | 5 589 | 8 339 | 2 598 | |
| 79 | 7 162 | 11 090 | 5 753 | 9 187 | 3 396 | |
| 100 | 7 279 | 9 225 | 5 904 | 7 717 | 4 472 | |
| 126 | 7 427 | 12 410 | 6 059 | 10 220 | 5 866 | |
| 158 | 7 600 | 13 090 | 6 141 | 10 900 | 7 888 | |
| 200 | 8 006 | 11 700 | 6 556 | 9 969 | 10 640 | |
| 251 | 8 146 | 15 660 | 6 672 | 13 060 | 14 280 | |
| 316 | 8 597 | 18 810 | 7 089 | 16 530 | 19 610 | |
| 398 | 9 501 | 20 550 | 8 078 | 18 120 | 27 650 | |
| 501 | 9 964 | 24 050 | 8 492 | 21 340 | 38 970 | |
| 631 | 11 070 | 38 790 | 9 510 | 35 720 | 55 540 | |
| 794 | 13 020 | 41 810 | 11 520 | 39 380 | 80 280 | |
| 1 000 | 14 660 | 50 870 | 13 130 | 48 230 | 118 000 | |
| 1 259 | 18 640 | 99 020 | 16 990 | 95 640 | 175 300 | |
| 1 585 | 25 300 | 113 500 | 23 660 | 110 800 | 263 000 | |
| 1 995 | 32 360 | 148 100 | 30 770 | 144 700 | 397 500 | |
| 2 512 | 45 540 | 314 800 | 43 980 | 311 400 | 608 800 | |
| 3 162 | 67 800 | 372 200 | 66 250 | 369 000 | 937 200 | |
| 3 981 | 98 560 | 491 500 | 96 780 | 488 100 | 1 457 000 | |
| 5 012 | 143 500 | 1 050 000 | 145 900 | 1 132 000 | 2 269 000 | |
| 6 310 | 214 100 | 1 284 000 | 227 700 | 1 357 000 | 3 546 000 | |
| 7 943 | 320 300 | 1 662 000 | 351 300 | 1 821 000 | 5 547 000 | |
| 10 000 | 466 400 | 3 519 000 | 538 400 | 4 382 000 | 8 700 000 | |
| 12 589 | 691 100 | 4 303 000 | 851 700 | 5 254 000 | 13 640 000 | |
| 15 849 | 1 007 000 | 5 481 000 | 1 310 000 | 7 079 000 | 21 440 000 | |
| 19 953 | 1 493 000 | 11 800 000 | 2 081 000 | 17 260 000 | 33 620 000 | |
| 25 119 | 2 185 000 | 13 620 000 | 3 296 000 | 20 710 000 | 53 030 000 | |
| 31 623 | 3 205 000 | 17 570 000 | 5 159 000 | 27 860 000 | 83 310 000 | |
| 39 811 | 4 637 000 | 36 800 000 | 8 109 000 | 68 540 000 | 131 500 000 | |
| 50 119 | 6 750 000 | 42 430 000 | 12 910 000 | 82 230 000 | 207 700 000 | |
| 63 096 | 9 913 000 | 54 770 000 | 20 410 000 | 110 600 000 | 326 900 000 | |
| 79 433 | 14 450 000 | 113 300 000 | 32 300 000 | 275 100 000 | 517 100 000 | |
| 100 000 | 20 800 000 | 130 600 000 | 51 640 000 | 330 700 000 | 819 700 000 | |
| 125 893 | 30 380 000 | 168 900 000 | 81 150 000 | 445 200 000 | 1 296 000 000 | |
| 158 489 | 44 090 000 | 346 800 000 | 129 200 000 | 1 103 000 000 | 2 058 000 000 | |
| 199 526 | 63 260 000 | 405 400 000 | 205 100 000 | 1 325 000 000 | 3 249 000 000 | |
| 251 189 | 92 330 000 | 517 300 000 | 325 100 000 | 1 766 000 000 | 5 153 000 000 | |
| 316 228 | 133 700 000 | 1 055 000 000 | 515 700 000 | 4 413 000 000 | 8 161 000 000 | |
| 398 107 | 191 900 000 | 1 228 000 000 | 815 500 000 | 5 311 000 000 | 12 930 000 000 | |
| 501 187 | 280 200 000 | 1 572 000 000 | 1 297 000 000 | 7 059 000 000 | 20 520 000 000 | |
| 630 957 | 404 900 000 | 3 181 000 000 | 2 061 000 000 | 17 570 000 000 | 32 570 000 000 | |
| 794 328 | 580 700 000 | 3 691 000 000 | 3 265 000 000 | 21 090 000 000 | 51 650 000 000 | |
| 1 000 000 | 846 100 000 | 4 724 000 000 | 5 182 000 000 | 28 310 000 000 | 82 000 000 000 | |
| 1 258 925 | 1 221 000 000 | 9 570 000 000 | 8 168 000 000 | 70 280 000 000 | 130 300 000 000 | |
| 1 584 893 | 1 750 000 000 | 11 050 000 000 | 12 970 000 000 | 84 120 000 000 | 207 300 000 000 | |
| 1 995 262 | 2 549 000 000 | 14 230 000 000 | 20 610 000 000 | 112 700 000 000 | 329 700 000 000 | |
| 2 511 886 | 3 676 000 000 | 28 800 000 000 | 32 610 000 000 | 279 900 000 000 | 525 100 000 000 | |
| 3 162 278 | 5 247 000 000 | 32 980 000 000 | 51 600 000 000 | 335 600 000 000 | ||
| 3 981 072 | 7 654 000 000 |
All the tests above were performed on an Intel Core 2 Quad Q6600 (2.40 GHz) CPU using a single thread, Windows XP SP 3, Java 1.6.0_22. Note that OpenJDK’s implementation of BigInteger.multiply() uses the naive \(Θ(n^2)\) algorithm in versions 7 and below, but has Karatsuba and other fast algorithms starting in 8.
Proofs
Matrix exponentiation
We will use weak induction to prove this identity.
- Base case
For \(n = 1\), clearly \( \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]^1 = \left[ \begin{matrix} F(2) & F(1) \\ F(1) & F(0) \end{matrix} \right] \).
- Induction step
-
Assume for \(n ≥ 1\) that \( \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]^n = \left[ \begin{matrix} F(n+1) & F(n) \\ F(n) & F(n-1) \end{matrix} \right] \). Then:
\( \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]^{n+1} \\ = \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]^n \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right] \\ = \left[ \begin{matrix} F(n+1) & F(n) \\ F(n) & F(n-1) \end{matrix} \right] \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right] \\ = \left[ \begin{matrix} F(n+1)+F(n) & F(n+1)+0 \\ F(n)+F(n-1) & F(n)+0 \end{matrix} \right] \\ = \left[ \begin{matrix} F(n+2) & F(n+1) \\ F(n+1) & F(n) \end{matrix} \right]. \)
Fast doubling
We will assume the fact that the matrix exponentiation method is correct for all \(n ≥ 1\).
\( \left[ \begin{matrix} F(2n+1) & F(2n) \\ F(2n) & F(2n-1) \end{matrix} \right] \\ = \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]^{2n} \\ = \left( \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]^n \right)^2 \\ = \left[ \begin{matrix} F(n+1) & F(n) \\ F(n) & F(n-1) \end{matrix} \right]^2 \\ = \left[ \begin{matrix} F(n+1)^2+F(n)^2 & F(n+1)F(n)+F(n)F(n-1) \\ F(n)F(n+1)+F(n-1)F(n) & F(n)^2+F(n-1)^2 \end{matrix} \right]. \)
Therefore, by equating cells in the top matrix to cells in the bottom matrix:
\(\begin{align} F(2n+1) &= F(n+1)^2 + F(n)^2. \\ F(2n) &= F(n) \left[ F(n+1) + F(n-1) \right] \\ &= F(n) \left[ F(n+1) + (F(n+1) - F(n)) \right] \\ &= F(n) \left[ 2F(n+1) - F(n) \right]. \\ F(2n-1) &= F(n)^2 + F(n-1)^2. \end{align}\)