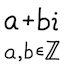 Factorize Gaussian integer (JavaScript)
Factorize Gaussian integer (JavaScript)
Program
Description
This JavaScript program calculates the prime factorization of the given Gaussian integer. A Gaussian integer is a complex number of the form a + bi, where a and b are integers. This program has a limit of |a|, |b| < 226. If the number is large, the program may hang for a few seconds.
The factorization is put into the following canonical form:
If the number is 0, 1, −1, i, or −i, then the factorization is the number itself.
Otherwise the factorization begins with a factor of −1 or i or −i if necessary. The rest are primes listed in ascending order of absolute value, breaking ties by lowest argument (angle); each of these factors has absolute value > 1 and are in the first quadrant (0 ≤ argument < π/2).
The source TypeScript code and compiled JavaScript code are available for viewing. A Java port of the code is also available.
Examples
- −1 = (−1). (unit)
- 2 = (−i) (1 + i) (1 + i).
- 4 + i = (4 + i). (complex prime)
- 7 = (7). (real prime)
- 5 + 9i = (1 + i) (7 + 2i).
Input format
The real or imaginary component can be suppressed, and they can be in either order. The 1 can be suppressed for i. For example, all these are valid inputs: 3, -0, -i, 5i, 1+i, 1+1i, -i-2, 4-0i
Spaces are allowed anywhere in the Gaussian integer, except within a string of digits.
To indicate negative numbers, the ASCII hyphen-minus (U+2D) and the minus sign (U+2212) are both acceptable. (The output properly uses the minus sign, though.)
j is an acceptable synonym for i, for those electrical engineers out there.
List of Gaussian primes
Table of all Gaussian primes up to norm 1000, with symmetries removed:
| Number | Norm | Argument |
|---|---|---|
| 1 + 1i | 2 | 45.00° |
| 2 + 1i | 5 | 26.57° |
| 3 + 0i | 9 | 0.00° |
| 3 + 2i | 13 | 33.69° |
| 4 + 1i | 17 | 14.04° |
| 5 + 2i | 29 | 21.80° |
| 6 + 1i | 37 | 9.46° |
| 5 + 4i | 41 | 38.66° |
| 7 + 0i | 49 | 0.00° |
| 7 + 2i | 53 | 15.95° |
| 6 + 5i | 61 | 39.81° |
| 8 + 3i | 73 | 20.56° |
| 8 + 5i | 89 | 32.01° |
| 9 + 4i | 97 | 23.96° |
| 10 + 1i | 101 | 5.71° |
| 10 + 3i | 109 | 16.70° |
| 8 + 7i | 113 | 41.19° |
| 11 + 0i | 121 | 0.00° |
| 11 + 4i | 137 | 19.98° |
| 10 + 7i | 149 | 34.99° |
| 11 + 6i | 157 | 28.61° |
| 13 + 2i | 173 | 8.75° |
| 10 + 9i | 181 | 41.99° |
| 12 + 7i | 193 | 30.26° |
| 14 + 1i | 197 | 4.09° |
| 15 + 2i | 229 | 7.59° |
| 13 + 8i | 233 | 31.61° |
| 15 + 4i | 241 | 14.93° |
| 16 + 1i | 257 | 3.58° |
| 13 + 10i | 269 | 37.57° |
| 14 + 9i | 277 | 32.74° |
| 16 + 5i | 281 | 17.35° |
| 17 + 2i | 293 | 6.71° |
| 13 + 12i | 313 | 42.71° |
| 14 + 11i | 317 | 38.16° |
| 16 + 9i | 337 | 29.36° |
| 18 + 5i | 349 | 15.52° |
| 17 + 8i | 353 | 25.20° |
| 19 + 0i | 361 | 0.00° |
| 18 + 7i | 373 | 21.25° |
| 17 + 10i | 389 | 30.47° |
| 19 + 6i | 397 | 17.53° |
| 20 + 1i | 401 | 2.86° |
| 20 + 3i | 409 | 8.53° |
| 15 + 14i | 421 | 43.03° |
| 17 + 12i | 433 | 35.22° |
| 20 + 7i | 449 | 19.29° |
| 21 + 4i | 457 | 10.78° |
| 19 + 10i | 461 | 27.76° |
| 22 + 5i | 509 | 12.80° |
| 20 + 11i | 521 | 28.81° |
| 23 + 0i | 529 | 0.00° |
| 21 + 10i | 541 | 25.46° |
| 19 + 14i | 557 | 36.38° |
| 20 + 13i | 569 | 33.02° |
| 24 + 1i | 577 | 2.39° |
| 23 + 8i | 593 | 19.18° |
| 24 + 5i | 601 | 11.77° |
| 18 + 17i | 613 | 43.36° |
| 19 + 16i | 617 | 40.10° |
| 25 + 4i | 641 | 9.09° |
| 22 + 13i | 653 | 30.58° |
| 25 + 6i | 661 | 13.50° |
| 23 + 12i | 673 | 27.55° |
| 26 + 1i | 677 | 2.20° |
| 26 + 5i | 701 | 10.89° |
| 22 + 15i | 709 | 34.29° |
| 27 + 2i | 733 | 4.24° |
| 26 + 9i | 757 | 19.09° |
| 20 + 19i | 761 | 43.53° |
| 25 + 12i | 769 | 25.64° |
| 22 + 17i | 773 | 37.69° |
| 26 + 11i | 797 | 22.93° |
| 28 + 5i | 809 | 10.12° |
| 25 + 14i | 821 | 29.25° |
| 27 + 10i | 829 | 20.32° |
| 23 + 18i | 853 | 38.05° |
| 29 + 4i | 857 | 7.85° |
| 29 + 6i | 877 | 11.69° |
| 25 + 16i | 881 | 32.62° |
| 23 + 20i | 929 | 41.01° |
| 24 + 19i | 937 | 38.37° |
| 29 + 10i | 941 | 19.03° |
| 28 + 13i | 953 | 24.90° |
| 31 + 0i | 961 | 0.00° |
| 31 + 4i | 977 | 7.35° |
| 31 + 6i | 997 | 10.95° |
All the prime numbers in the table above are located in the first octant – a number has the form a + bi and satisfies a > 0, b ≥ 0, and a ≥ b (thus the argument is in the range [0, π/4)). They are listed in order of ascending norm, with ties broken by ascending argument. (“Norm” means squared absolute value, which is |a + bi| = a2 + b2.)
For each prime, a set of up to seven symmetrical primes have been excluded from the list. This is because if z is prime, then so are −z, iz, −iz, z (conjugate), −z, iz, and −iz. In terms of components, if z = a + bi is prime, then respectively so are −a − bi, −b + ai, b − ai, a − bi, −a + bi, b + ai, and −b − ai.
For example, 3 is prime, therefore so are −3, 3i, and −3i. For example, 5 + 2i is prime, therefore so are −5 − 2i, −2 + 5i, 2 − 5i, 5 − 2i, −5 + 2i, 2 + 5i, and −2 − 5i.