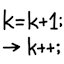Project Nayuki

Example of simplifying and improving code

When I see program code that can be simplified or improved, I seize the opportunity to make those changes. I’m passionate about working with code that is small and easy to understand, and abhor code that is unnecessarily complicated, long, or overly clever.

I practice code simplification all the time – in my personal programming projects, school homework, occasional participation in open-source projects, and coding in the workplace. I come across bad code on a regular basis (especially at most jobs), so in this article I hope to illustrate an example of how I apply my skills to clean up poor code.

Contents

Original program code

This is Rian J Stockbower’s solution to Project Euler problem #21 (used without permission; contacted with no response). File: Problem021-0.java

import java.util.ArrayList;
import java.util.Iterator;
 
public class Problem021
{
    private static int MSum;
    private static int NSum;
 
    private static int sumList(ArrayList<Integer> list)
    {
        int sum = 0;
 
        for (Iterator<Integer> iter = list.iterator(); iter.hasNext();)
        {
            sum += iter.next();
        }
 
        return sum;
    }
 
    private static ArrayList<Integer> createList(int n)
    {
        // Creates a list of integers that evenly divide into n excluding n itself
        long root = Math.round(Math.sqrt(n)) + 1;
 
        ArrayList<Integer> test = new ArrayList<Integer>();
        test.add(1);
 
        for (int i = 2; i <= root; i++)
        {
            if (n % i == 0)
            {
                test.add(i);        // Add the divisor & its complement
                test.add(n/i);
            }
        }
 
        return test;
    }
 
    private static boolean isAmicable(int n)
    {
        /*** If n's divisors form an amicable set, return true ***/
 
        // Create a list of n's proper divisors
        ArrayList<Integer> NList = new ArrayList<Integer>(createList(n));        
 
        // Sum n's proper divisors (NSum)
        NSum = sumList(NList);
 
        // Create list of NSum's proper divisors (MList)
        ArrayList<Integer> MList = new ArrayList<Integer>(createList(NSum));
 
        // Sum m's proper divisors (MSum)
        MSum = sumList(MList);
 
        if ((MSum == n) && (MSum != NSum))
            return true;    
 
        return false;
    }
 
    public static void main(String[] args)
    {
        long begin = System.currentTimeMillis();
 
        int sum = 0;
        for (int i = 0; i < 10000; i++)
        {
            if (isAmicable(i))
            {
                sum += NSum;
            }
        }
 
        System.out.println(sum);
 
        long end = System.currentTimeMillis();
        System.out.println(end-begin + "ms");
    }
}

Local changes

These small changes can be made by only considering a few lines of code at a time. They’re easy to understand and easy to verify for correctness.

For-each loop

If we’re using generics, then we’re using Java SE 5+, which means the for-each loop is also supported. We should use the enhanced for statement to eliminate the boring boilerplate code of using an explicit iterator. This makes the import statement for java.util.Iterator no longer needed. Also, we take advantage of auto-unboxing to use the int type rather than Integer. Afterward, since the loop has very few tokens, I prefer to eliminate the braces too.

import java.util.Iterator;
...
for (Iterator<Integer> iter = list.iterator(); iter.hasNext();)
{
    sum += iter.next();
}

Revised:

for (int x : list)
    sum += x;

Unnecessary parentheses

We know that == and != have a higher precedence than &&. Using equality and logical operators in the same expression is so common that it pays to learn this precedence by heart. Thus we should remove the unnecessary parentheses here.

if ((MSum == n) && (MSum != NSum))

Revised:

if (MSum == n && MSum != NSum)

Unnecessary if+return

Using an if-statement to return a Boolean true/false value is redundant. We can take the condition of the if-statement and return it directly instead.

if (MSum == n && MSum != NSum)
    return true;
return false;

Revised:

return MSum == n && MSum != NSum;

Recommended parentheses

This expression is correct but brittle – for example, if we add a string in front (e.g. print("Time: " + end-begin + "ms")), then it’ll fail to compile. So it’s a good idea to add parentheses here.

System.out.println(end-begin + "ms");

Revised:

System.out.println((end-begin) + "ms");

Non-Javadoc comment

Because this comment starts with /**, it’s syntactically a Javadoc comment. But Javadoc comments are only applicable to classes, interfaces, enums, fields, methods, and constructors – not to local variables. This comment would appear to document the local variable NList, but this isn’t supported and the content of the comment is unrelated to NList anyhow. Also, some text editors show Javadoc comments differently from regular comments, so this is misleading. Let’s remove the extra stars in the comment.

/*** If n's divisors form an amicable set, return true ***/
// Create a list of n's proper divisors
ArrayList<Integer> NList = new ArrayList<Integer>(createList(n));

Revised:

/* If n's divisors form an amicable set, return true */
// Create a list of n's proper divisors
ArrayList<Integer> NList = new ArrayList<Integer>(createList(n));

After local changes

After performing the five changes above, plus deleting {a pair of braces, a few trailing tabs, and blank lines}, we get Problem021-1.java.

Contextual changes

These changes take data flow and global usage into consideration. They do not change the values that are computed by the program.

Eliminating copies

In isAmicable(), the return value of createList() is fed into the constructor for a new ArrayList. This extra copy is unnecessary because the (actual) return type of createList() is already ArrayList, and the data is already a unique (non-shared) copy.

ArrayList<Integer> NList = new ArrayList<Integer>(createList(n));
...
ArrayList<Integer> MList = new ArrayList<Integer>(createList(NSum));

Revised:

ArrayList<Integer> NList = createList(n);
...
ArrayList<Integer> MList = createList(NSum);

Merging functions

As we see in isAmicable(), the function sumList() is always called with the result of createList(). Also, the result of createList() is never used in any other way. Since createList() and sumList() aren’t public API methods that external code might call, we can merge the functionality of sumList() into createList(), then rename the function more appropriately to divisorSum().

import java.util.ArrayList;
...
private static int sumList(ArrayList<Integer> list)
{
    int sum = 0;
    for (int x : list)
        sum += x;
    return sum;
}

private static ArrayList<Integer> createList(int n)
{
    // Creates a list of integers that evenly divide into n excluding n itself
    long root = Math.round(Math.sqrt(n)) + 1;

    ArrayList<Integer> test = new ArrayList<Integer>();
    test.add(1);

    for (int i = 2; i <= root; i++)
    {
        if (n % i == 0)
        {
            test.add(i);        // Add the divisor & its complement
            test.add(n/i);
        }
    }

    return test;
}

private static boolean isAmicable(int n)
{
    /* If n's divisors form an amicable set, return true */

    // Create a list of n's proper divisors
    ArrayList<Integer> NList = createList(n);

    // Sum n's proper divisors (NSum)
    NSum = sumList(NList);

    // Create list of NSum's proper divisors (MList)
    ArrayList<Integer> MList = createList(NSum);

    // Sum m's proper divisors (MSum)
    MSum = sumList(MList);

    return MSum == n && MSum != NSum;
}

Revised:

private static int divisorSum(int n)
{
    // Finds the sum of integers that evenly divide into n excluding n itself
    long root = Math.round(Math.sqrt(n)) + 1;

    int sum = 1;
    for (int i = 2; i <= root; i++)
    {
        if (n % i == 0)
        {
            sum += i;        // Add the divisor & its complement
            sum += n/i;
        }
    }
    return sum;
}

private static boolean isAmicable(int n)
{
    /* If n's divisors form an amicable set, return true */

    // Sum n's proper divisors (NSum)
    NSum = divisorSum(n);

    // Sum m's proper divisors (MSum)
    MSum = divisorSum(NSum);

    return MSum == n && MSum != NSum;
}

Narrowing scope

The variable MSum is only used in isAmicable(), and it’s written before it’s read. It only needs to be visible within isAmicable() and doesn’t need to carry state from one call to the next. Thus we can narrow its scope (and lifetime) from the class level (static field) to the method level (local variable). This has the side effect of making isAmicable() safely reentrant for potentially recursive or concurrent calls.

The variable NSum is written and read in the same way within isAmicable(), but it’s also read in main() immediately after calling isAmicable(). We can narrow its scope in the same way, but in main() we need to compute the value of NSum afresh.

private static int MSum;
private static int NSum;
...
private static boolean isAmicable(int n)
{
    ...
    NSum = divisorSum(n);
    ...
    MSum = divisorSum(NSum);
    ...
}
...
public static void main(String[] args)
{
    ...
        if (isAmicable(i))
            sum += NSum;

Revised:

private static boolean isAmicable(int n)
{
    ...
    int NSum = divisorSum(n);
    ...
    int MSum = divisorSum(NSum);
    ...
}
...
public static void main(String[] args)
{
    ...
        if (isAmicable(i))
            sum += divisorSum(i);

Reworking logic

In isAmicable(), we effectively examine a sequence of three numbers (n, NSum, MSum) – the function returns true iff the first is equal to the third but the second is unequal to the third. We can change the “but” part to “the first is unequal to the second”, to yield some gains later on.

Proof that MSum == n && MSum != NSum is logically equivalent to MSum == n && n != NSum: In the case that MSum == n, by substitution we have MSum != NSum being logically equivalent to n != NSum. Otherwise with MSum != n, both expressions are identically false.

return MSum == n && MSum != NSum;

Revised:

return MSum == n && n != NSum;

Inlining variable

Now that isAmicable() only has one usage of MSum, we can inline its declared value into the single usage. We reverse the two conditions because neither has a (real) side effect, and it’s more efficient to skip the expensive call to divisorSum() if the simple integer comparison fails first.

Also, we rename NSum to nSum because Java’s style convention states that local variables start with a lowercase letter. Finally, we eliminate all the comments – the opening comment is implied by the function name, and the two other comments don’t describe the code well.

private static boolean isAmicable(int n)
{
    /* If n's divisors form an amicable set, return true */

    // Sum n's proper divisors (NSum)
    int NSum = divisorSum(n);

    // Sum m's proper divisors (MSum)
    int MSum = divisorSum(NSum);

    return MSum == n && n != NSum;
}

Revised:

private static boolean isAmicable(int n)
{
    int nSum = divisorSum(n);
    return n != nSum && divisorSum(nSum) == n;
}

After contextual changes

After performing the five changes above, we get Problem021-2.java.

Semantic changes

These major changes involve an understanding of the problem domain, and often visibly change the behavior of the program or subfunctions.

Revising divisorSum()

This function is subtly incorrect in two ways. The for-loop should only search up to and including floor(√n), but in the code it can go up to and including floor(√n) + 2 due to the rounding and the +1. For example, for n = 3, root = 3, but we actually want root = floor(√3) = 1. The wrong search range means that extra factors are considered, which does make the final sum incorrect in some cases (e.g. n = 2, 3).

Secondly, if n is a perfect square and i = √n, then i = n/i, so they are not two distinct factors. We need to detect and handle this special case.

Other points: √n ≤ n. Since n is int, we can fit √n in int too (no need for long; the author probably did this because Math.round() returns long). By luck, the old incorrect divisorSum() algorithm doesn’t seem to cause isAmicable() to be wrong for any number, so it doesn’t affect the program’s final answer.

private static int divisorSum(int n)
{
    // Finds the sum of integers that evenly divide into n excluding n itself
    long root = Math.round(Math.sqrt(n)) + 1;

    int sum = 1;
    for (int i = 2; i <= root; i++)
    {
        if (n % i == 0)
        {
            sum += i;        // Add the divisor & its complement
            sum += n/i;
        }
    }
    return sum;
}

Revised:

private static int divisorSum(int n)
{
    // Finds the sum of integers that evenly divide into n excluding n itself
    int root = (int)Math.sqrt(n);

    int sum = 1;
    for (int i = 2; i <= root; i++)
    {
        if (n % i == 0)
        {
            sum += i;        // Add the divisor & its complement
            if (i * i != n)
                sum += n/i;
        }
    }
    return sum;
}

Revising the sum

From the problem statement, we know that amicable numbers come in pairs (a, b), where a ≠ b. The way the original program was written, if a is amicable then b is added to the sum. We should be more direct and add a to the sum instead. This eliminates a function call and is truer to the problem statement’s intent. Moreover, if a < 10000 but b ≥ 10000, then it matters which number is added to the sum. (By luck, this is not an issue. But if the problem’s upper bound were 5200, then this would cause a discrepancy.)

if (isAmicable(i))
    sum += divisorSum(i);

Revised:

if (isAmicable(i))
    sum += i;

Final program code

File: Problem021-3.java

public class Problem021
{
    private static int divisorSum(int n)
    {
        // Finds the sum of integers that evenly divide into n excluding n itself
        int root = (int)Math.sqrt(n);

        int sum = 1;
        for (int i = 2; i <= root; i++)
        {
            if (n % i == 0)
            {
                sum += i;        // Add the divisor & its complement
                if (i * i != n)
                    sum += n/i;
            }
        }
        return sum;
    }

    private static boolean isAmicable(int n)
    {
        int nSum = divisorSum(n);
        return n != nSum && divisorSum(nSum) == n;
    }

    public static void main(String[] args)
    {
        long begin = System.currentTimeMillis();

        int sum = 0;
        for (int i = 0; i < 10000; i++)
        {
            if (isAmicable(i))
                sum += i;
        }
        System.out.println(sum);

        long end = System.currentTimeMillis();
        System.out.println((end-begin) + "ms");
    }
}

Additional comments

In this article, we took a piece of code and walked through the process of how I would simplify it, clean it up, and fix errors, one step at a time. The size of the program started at 81 lines of code and went down to 42 lines.

By comparison, here is my own Java solution for this same Project Euler problem #21 (I wrote this Java code a year before this article). As we can see, the structure is extremely similar – 3 major functions and an essentially identical isAmicable() function – though my code uses a different brace style, a top-down arrangement of functions, and a slower non-square-root divisorSum() for simplicity. When I write code I naturally simplify as I go along, so everything that is committed to version control is already simplified; almost none of my intermediate work is archived. So it’s normal for my code to uphold a high level of quality all the time.

It was hard to find a suitable piece of code for this article – it needed to be short, have many opportunities for improvement, and be non-confidential. I typically see enough improvement opportunities in code that’s about 300 to 1000 lines long, but just the scrolling would likely bore a reader to death. Most short programs I encounter don’t have enough improvement opportunities. Also, I have many examples of bad code from the workplace but not many from public sources, however workplace code is confidential. In the worst case I might have chosen to fabricate bad code by mashing up various real examples I actually worked with, but it would feel rather unnatural and contrived. So it was very fortunate that I ran into this piece of code, which more than met my requirements.

Here an example from another author, who took a verbose and sloppy piece of code and turned it into something concise and self-evident. He shows the original code and revised code, and justifies why the new logic is functionally equivalent to the old logic. Link: 8th Light: Fecophiles.

What do you think – does code simplicity matter? Is it helpful or is it a waste of time? Maybe the discussion of this topic will inspire you to aim for perfection in your code craft.

More info