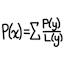Project Nayuki

Computing Wikipedia’s internal PageRanks

Java program run for Wikipedia PageRank

Introduction

Wikipedia is the world’s largest online encyclopedia, comprising millions of pages and links between pages. It also gives away all of this data in an easy-to-process format, via its periodic database dumps. What would happen if we took this set of data and ran the classic PageRank algorithm on every single page?

PageRank is a method for determining the importance of each document in a web of linked documents. Given a set of documents and the set of directed links between them, we can calculate the PageRank of each document using some simple arithmetic (or linear algebra).

I was motivated to calculate the PageRank of each page on Wikipedia for several reasons:

  • In the MediaWiki software that powers Wikipedia, the “What links here” tool shows a list of pages in an arbitrary, not-very-useful order. I wanted to see whether sorting that list by descending PageRank would yield better results.

  • Wikipedia is among the few interesting sites that publish dumps of its database, so it’s possible to download the necessary data without doing messy web scraping (which is slow, requires lots of ad hoc processing, and is generally prohibited by most websites).

  • I have no prior experience handling “big data” (nor MapReduce, etc.), and this would be my first time working with a data set with a hundred million items, using only low-level operations. Here I would see firsthand how to use memory judiciously and what considerations are needed to work on big data.

(While this idea of calculating Wikipedia PageRanks is not new and other people’s published work can be readily found on the web, the specific approach and details are interesting enough that I’d like to share how I did it.)

Results

Top pages

The PageRank of a document is the probability that a visitor will end up at that document after uniform random browsing. As such, the sum of all the PageRanks in the set of documents must equal 1. Because probabilities can get very small, the base-10 logarithm of the PageRank will be shown instead of the raw probability.

A list of the top 10 000 pages on English Wikipedia, along with the log10 PageRanks in descending order: wikipedia-top-pageranks.txt

A treemap of the (linear) probabilities of the top 1000 pages (these account for 7.3% of the total probability):

Treemap of Wikipedia's top 1000 pages

Sorting “What links here”

As mentioned in the introduction, my original motivation for computing PageRanks was to sort the “What links here” list of pages by PageRank. For the arbitrarily chosen page Telescope (as of ), here are the links in MediaWiki’s order (with various data cleanup) versus in descending PageRank order.

We can see that the original order starts off alphabetically, then becomes a mess of obscure people, places, and concepts with random clusters. By contrast, the PageRanked list shows familiar general concepts for the first hundred results, just as we would expect. This ordered list is useful for playing the game Six Degrees of Wikipedia from human memory, because we can learn to better predict where a page’s incoming links come from.

Computation statistics
  • Number of pages (filtered): 10 703 129
  • Number of links (filtered): 320 320 061
  • Time per PageRank iteration: 5.2 seconds
    (run on Intel Core i5-2450M 2.50 GHz, Windows 7 Pro SP1, Java 64-bit 1.7.0_25)
  • Iterations to convergence: Approximately 250
  • Total CPU time: About 30 minutes (mostly spent on parsing SQL data values, less spent on computing PageRank)

(All my results are computed from the dump.)

Program implementation

Language choice

Handling the Wikipedia page link data set would involve storing and manipulating tens or hundreds of millions of items in memory, so this consideration heavily influenced what programming language I would use to solve the problem:

  • Python (CPython) is slow for arithmetic operations (about 1/30× the speed of C/C++) and is memory-inefficient (e.g. a list of integers uses far more than 4 bytes per element). Python would be usable for this problem only if I used NumPy, which packs numbers in memory efficiently and has fast vector operations. But still, custom non-vector operations can only be computed at Python speed instead of C speed. On the plus side, Python code is concise and powerful, and its interactive interpreter (REPL) lets you keep data loaded in memory while trying out new code (without the long compile-rerun cycle).

  • C/C++ handles big data sets well – there’s precise control over how much memory each data element uses, and the compiler generates code that executes quickly. However, writing memory-safe code is tricky (careful explicit bounds-checking, etc.), debugging undefined behavior can be confusing, handling error conditions / exceptions (especially I/O) is clumsy, external libraries need to be compiled and linked for functionality like gzip, and writing portable cross-platform code is a headache. Also C/C++ poorly supports Unicode and UTF-8, requiring a conscious effort to use Unicode-aware libraries for string handling.

  • Java provides the right middle ground for this problem, in my carefully considered opinion. It stores arrays of numbers in an efficient packed representation just like C/C++, and the JIT-compiled bytecode runs fast enough at about 1/2× the speed of C/C++ (without SIMD). Programs can run on 32-bit and 64-bit systems without any effort on the programmer’s part. It has precise array bounds checking, comes with free stack traces for crash analysis, and has a clean exception mechanism. Moreover, Java has a built-in library for gzip decompression, which proves to be extremely convenient in this case.

After choosing Java and writing the program, I noticed some drawbacks of this approach. Storing the mapping of page titles (strings) to IDs (ints) was very memory-heavy, weighing at roughly 500 bytes per entry (for 10 million entries). During the data loading phase, there were many spikes of high CPU usage and frozen program execution because of garbage collection. Normally the Java GC fades into the background, but when dealing with millions of objects stored in gigabytes of memory, GC does start to show its ugly side. However after the SQL text has been parsed and the data has been preprocessed, the rest of the program executes smoothly. Although the high memory usage and GC pauses were undesirable, these were not sufficient reasons to prefer Python or C or C++ over Java for implementing this PageRank application.

Program architecture

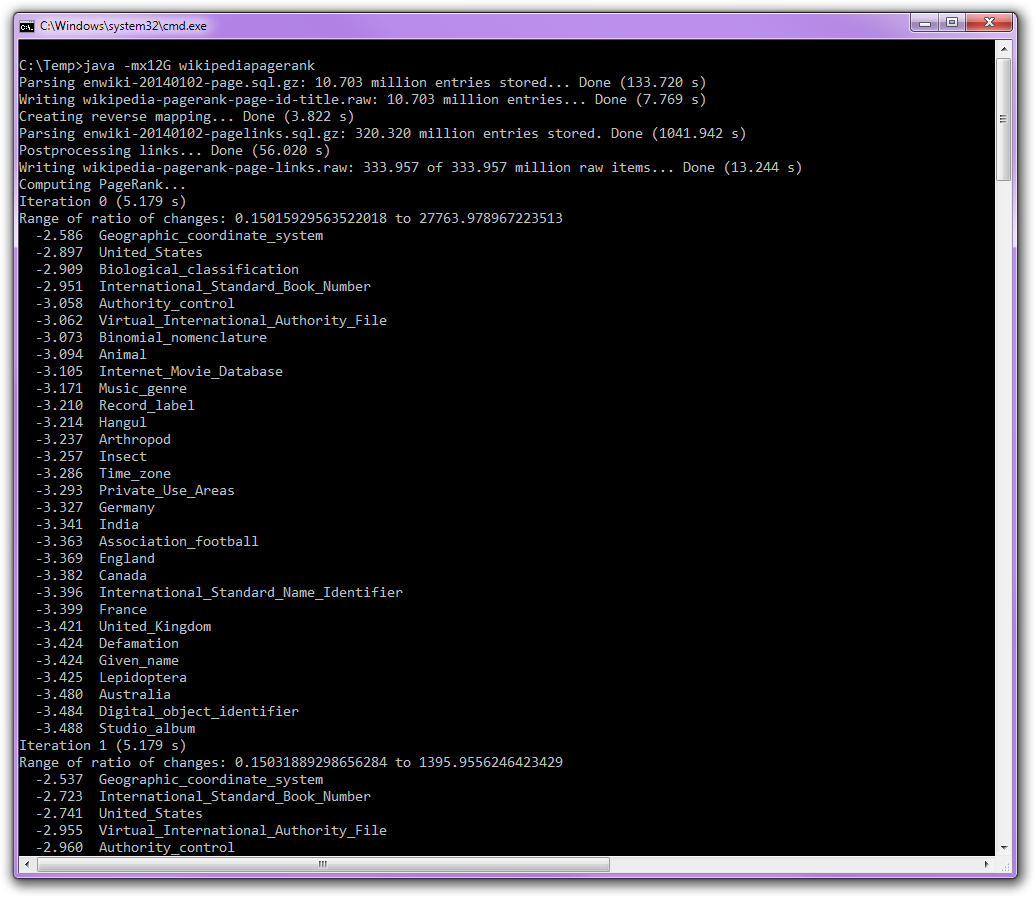
Here is a high-level view of how my program works:

  1. Read the file enwiki-yyyymmdd-page.sql.gz, decompress gzip on the fly, parse the SQL text to extract the tuples of (string page title, int page ID), filter out entries that are not in namespace #0, and store them in memory in a Map<String,Integer>.

  2. Read the file enwiki-yyyymmdd-pagelinks.sql.gz, decompress gzip on the fly, parse the SQL text to extract the tuples, filter out tuples whose target is not a known page or not in namespace #0, represent each link as (int source page ID, int target page ID), and store them in memory in a long[].

  3. Sort the list of page links so that memory will be accessed in a more cache-friendly order, and repack them into a more compact format. First sort by link target ID, then group the entries together using a kind of run-length encoding.

    For example, if we have the list of page links [(5,0), (1,0), (3,2), (4,0)], then sorting it by target page ID (breaking ties by source ID) gives [(1,0), (4,0), (5,0), (3,2)]. Grouping the links by target ID into the format (target page ID, number of incoming links, source page IDs...) gives [(0,3,1,4,5), (2,1,3)] (i.e. page 0 has 3 incoming links {1,4,5}, and page 2 has 1 incoming link {3}).

  4. Do 1000 iterations of the PageRank computation. At each iteration, print a bunch of top-ranking pages. Also print the amount of change per iteration to let the user manually monitor the progress, to see if the numbers converged. The arithmetic formula for calculating PageRank is well-known and is explained better by Wikipedia and other sources, so this is what I won’t describe on this page.

  5. Write out all the PageRanks to a file (starting at page ID 0, then 1, 2, 3, etc.). This allows the data from this expensive computation to be loaded for later analysis.

Notes:

  • The SQL files (after decompressing from gzip) are plain text files containing comments and SQL commands. There is a CREATE TABLE command that defines the table schema, and there is a huge bunch of INSERT INTO commands (one per line at about 1 MB of text per line) that populate the new table with data. Here are previews of these SQL files, if you want to get an idea of the incoming data format: enwiki-20140102-page-preview.sql, enwiki-20140102-pagelinks-preview.sql

  • The decompressed file sizes are 3.04 GB for enwiki-20140102-page.sql, and 27.66 GB for enwiki-20140102-pagelinks.sql.

  • Namespace #0 is for articles. The other ones are for Talk, User, Help, etc.

Room for improvement

This program meets my needs for the problem at hand, and it handles the data and most edge cases correctly. However, there’s still room for improvement when it comes to flexibility and time/space efficiency.

  • Instead of using a hand-coded FSM, make the SQL parsing less brittle and code it at a higher level. Perhaps use a real SQL parser library, or at least have a proper lexer and context-free grammar parser.

  • Pack the string/int map into a much more compact format, because this is the biggest memory hog. This basically means writing a custom class that implements the interface Map<String,Integer>.

  • Check for integer overflows, memory allocations that would exceed the signed 32-bit size limit, divisions by zero, etc.

  • Multithread the computations for SQL parsing and for PageRank iterations.

Source code and instructions

Java source code:

English Wikipedia data dumps: https://dumps.wikimedia.org/enwiki/
From a snapshot of your choice, download the two files enwiki-yyyymmdd-page.sql.gz (~1 GB) and enwiki-yyyymmdd-pagelinks.sql.gz (~5 GB). Update the file names at the top of WikipediaPagerank.java and compile.

To run this program on the Wikipedia data set, you must use a 64-bit JVM and have about 12 GiB of free RAM on your computer. Put the Java class files and the .sql.gz files in the same directory. Run with the command java -mx12G WikipediaPagerank . If the program execution runs out of memory, then increase the “12G” further.

When each .sql.gz file is loaded for the first time, the data is parsed and filtered, and then the program caches the data by writing a temporary .raw file. In subsequent runs, the cached version loads much faster than the original .sql.gz file, because the data (strings and int32) is loaded directly – without needing to decompress gzip, parse the SQL text (the slowest part), or filter out unneeded data. Note that wikipedia-pagerank-page-id-title.raw will be ~0.3 GB and wikipedia-pagerank-page-links.raw will be ~1.5 GB, so make sure you have enough storage space available for these temporary files.

More info