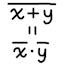Boolean algebra laws
PDF versionNotation
The following notation is used for Boolean algebra on this page, which is the electrical engineering notation:
- False: 0
- True: 1
- NOT x: x
- x AND y: x ⋅ y
- x OR y: x + y
- x XOR y: x ⊕ y
The precedence from high to low is AND, XOR, OR. Examples:
- x + y ⋅ z means x + (y ⋅ z)
- x ⊕ y ⋅ z means x ⊕ (y ⋅ z)
- x + y ⊕ z means x + (y ⊕ z)
Basic laws
Constants
- NOT:
- 0 = 1
- 1 = 0
- AND:
- 0 ⋅ 0 = 0
- 0 ⋅ 1 = 0
- 1 ⋅ 0 = 0
- 1 ⋅ 1 = 1
- OR:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 1
- XOR:
- 0 ⊕ 0 = 0
- 0 ⊕ 1 = 1
- 1 ⊕ 0 = 1
- 1 ⊕ 1 = 0
Constant and variable
- AND:
- 0 ⋅ x = 0
- 1 ⋅ x = x
- OR:
- 0 + x = x
- 1 + x = 1
- XOR:
- 0 ⊕ x = x
- 1 ⊕ x = x
One variable
- NOT:
- NOT x = x
- AND:
- x ⋅ x = x
- x ⋅ x = 0
- OR:
- x + x = x
- x + x = 1
- XOR:
- x ⊕ x = 0
- x ⊕ x = 1
XOR
XOR can be defined in terms of AND, OR, NOT:
- x ⊕ y = (x ⋅ y) + (x ⋅ y)
- x ⊕ y = (x + y) ⋅ (x + y)
- x ⊕ y = (x + y) ⋅ (x ⋅ y)
Commutativity
- AND: x ⋅ y = y ⋅ x
- OR: x + y = y + x
- XOR: x ⊕ y = y ⊕ x
Associativity
- AND: (x ⋅ y) ⋅ z = x ⋅ (y ⋅ z)
- OR: (x + y) + z = x + (y + z)
- XOR: (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z)
Distributivity
- x ⋅ (y + z) = (x ⋅ y) + (x ⋅ z)
- x + (y ⋅ z) = (x + y) ⋅ (x + z)
- x ⋅ (y ⊕ z) = (x ⋅ y) ⊕ (x ⋅ z)
De Morgan’s laws
- NAND: x ⋅ y = x + y
- NOR: x + y = x ⋅ y
Redundancy laws
The following laws will be proved with the basic laws. Counter-intuitively, it is sometimes necessary to complicate the formula before simplifying it.
Absorption
-
x + x ⋅ y = x
Proof:
x + x ⋅ y
= x ⋅ 1 + x ⋅ y
= x ⋅ (1 + y)
= x ⋅ 1
= x -
x ⋅ (x + y) = x
Proof:
x ⋅ (x + y)
= (x + 0) ⋅ (x + y)
= x + (0 ⋅ y)
= x + 0
= x
No name
-
x + x ⋅ y = x + y
Proof:
x + x ⋅ y
= (x + x) ⋅ (x + y)
= 1 ⋅ (x + y)
= x + y -
x ⋅ (x + y) = x ⋅ y
Proof:
x ⋅ (x + y)
= x ⋅ x + x ⋅ y
= 0 + x ⋅ y
= x ⋅ y -
x ⋅ y + x ⋅ y = x
Proof:
x ⋅ y + x ⋅ y
= x ⋅ (y + y)
= x ⋅ 1
= x -
(x + y) ⋅ (x + y) = x
Proof:
(x + y) ⋅ (x + y)
= x + (y ⋅ y)
= x + 0
= x
Consensus
-
x ⋅ y + x ⋅ z + y ⋅ z = x ⋅ y + x ⋅ z
Proof:
x ⋅ y + x ⋅ z + y ⋅ z
= x ⋅ y + x ⋅ z + 1 ⋅ y ⋅ z
= x ⋅ y + x ⋅ z + (x + x) ⋅ y ⋅ z
= x ⋅ y + x ⋅ z + x ⋅ y ⋅ z + x ⋅ y ⋅ z
= x ⋅ y + x ⋅ y ⋅ z + x ⋅ z + x ⋅ y ⋅ z
= x ⋅ y ⋅ 1 + x ⋅ y ⋅ z + x ⋅ 1 ⋅ z + x ⋅ y ⋅ z
= x ⋅ y ⋅ (1 + z) + x ⋅ z ⋅ (1 + y)
= x ⋅ y ⋅ 1 + x ⋅ z ⋅ 1
= x ⋅ y + x ⋅ z -
(x + y) ⋅ (x + z) ⋅ (y + z) = (x + y) ⋅ (x + z)
Proof:
(x + y) ⋅ (x + z) ⋅ (y + z)
= (x + y) ⋅ (x + z) ⋅ (0 + y + z)
= (x + y) ⋅ (x + z) ⋅ (x ⋅ x + y + z)
= (x + y) ⋅ (x + z) ⋅ (x + y + z) ⋅ (x + y + z)
= (x + y) ⋅ (x + y + z) ⋅ (x + z) ⋅ (x + y + z)
= (x + y + 0) ⋅ (x + y + z) ⋅ (x + 0 + z) ⋅ (x + y + z)
= (x + y + 0 ⋅ z) ⋅ (x + z + 0 ⋅ y)
= (x + y + 0) ⋅ (x + z + 0)
= (x + y) ⋅ (x + z)