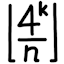Project Nayuki

Barrett reduction algorithm

If we want to compute many instances of \(ab \text{ mod } n\) for a fixed modulus \(n\) (where \(0 ≤ ab < n^2\)), we can avoid the slowness of long division and instead perform these modular reductions using the Barrett reduction algorithm. For the given \(n\) we precompute a factor using division; thereafter the computations of \(ab \text{ mod } n\) only involve multiplications, subtractions, and shifts (all of which are faster operations than division).

Algorithm

Precomputation:

  1. Assume the modulus \(n ∈ \mathbb{N}\) is such that \(n \geq 3\) and \(n\) is not a power of 2.
    (This is for the sake of the proof below, and because modulo-power-of-2 is trivial.)

  2. Choose \(k ∈ \mathbb{N}\) such that \(2^k > n\). (The smallest choice is \(k = \lceil \log_2 n \rceil\).)

  3. Calculate \(r = \left\lfloor \frac{4^k}{n} \right\rfloor\). (This is the precomputed factor.)

Reduction:

  1. We are given \(x ∈ \mathbb{N}\), such that \(0 ≤ x < n^2\), as the number that needs to be reduced modulo \(n\).

  2. Calculate \(t = x - \left\lfloor \frac{xr}{4^k} \right\rfloor n\).

  3. If \(t < n\) then return \(t\), else return \(t - n\). This answer is equal to \(x \text{ mod } n\).

Proof of correctness

  1. Since \(n\) is not a power of 2, we know \(\frac{4^k}{n}\) is not an integer.
    Thus \(\frac{4^k}{n} - 1 < r < \frac{4^k}{n}\).

  2. Multiply by \(x\) (\(x \geq 0\)): \(x \left( \frac{4^k}{n} - 1 \right) ≤ xr ≤ x \frac{4^k}{n}\).

  3. Divide by \(4^k\): \(\frac{x}{n} - \frac{x}{4^k} ≤ \frac{xr}{4^k} ≤ \frac{x}{n}\).

  4. Because \(x < n^2 < 4^k\), we know \(\frac{x}{4^k} < 1\).
    Therefore: \(\frac{x}{n} - 1 < \frac{xr}{4^k} ≤ \frac{x}{n}\).

  5. One floor: \(\frac{x}{n} - 2 < \left\lfloor \frac{x}{n} - 1 \right\rfloor\).
    Another floor: \(\left\lfloor \frac{x}{n} - 1 \right\rfloor ≤ \left\lfloor \frac{xr}{4^k} \right\rfloor\).
    Put together: \(\frac{x}{n} - 2 < \left\lfloor \frac{x}{n} - 1 \right\rfloor ≤ \left\lfloor \frac{xr}{4^k} \right\rfloor ≤ \frac{x}{n}\).

  6. Multiply by \(n\) (\(n > 0\)): \(x - 2n < \left\lfloor \frac{xr}{4^k} \right\rfloor n ≤ x\).

  7. Negate: \(-x ≤ -\left\lfloor \frac{xr}{4^k} \right\rfloor n < 2n - x\).

  8. Add \(x\): \(0 ≤ x - \left\lfloor \frac{xr}{4^k} \right\rfloor n < 2n\).

  9. Clearly \(x ≡ x - \left\lfloor \frac{xr}{4^k} \right\rfloor n \text{ mod } n\), because \(\left\lfloor \frac{xr}{4^k} \right\rfloor n\) is a multiple of \(n\).

  10. The algorithm up to this point correctly reduces \(x\) from the range \([0, n^2)\) to \(t\) in the range \([0, 2n)\) without changing its congruence modulo \(n\). The fix-up in the final step is simple, to get the desired answer in the range \([0, n)\).

Bit width analysis

This is helpful for fixed-size bigint implementations and to predict the running time.

  1. Assume the modulus is exactly \(m\) bits long, i.e. \(2^{m-1} < n < 2^m\).

  2. Often we want to set \(k = m\), but let’s allow the general case of \(k \geq m\).

  3. Then \(4^k = 2^{2k}\) is \(2k + 1\) bits long.

  4. Reciprocal: \(2^{-m} < \frac{1}{n} < 2^{1-m}\).

  5. Multiply by \(4^k\): \(2^{2k-m}\) < \(\frac{4^k}{n} < 2^{2k-m+1}\).
    Therefore \(r\) is \(2k - m + 1\) bits long. (If \(k = m\), then \(r\) is \(k + 1\) bits.)

  6. We know \(0 ≤ x < n^2\) fits in \(2m\) bits, thus \(xr\) fits in \(2k + m + 1\) bits.

  7. But in fact, \(xr < x \frac{4^k}{n} < 4^k n\), where \(4^k n\) is known to be exactly \(2k + m\) bits.
    Therefore \(xr\) fits in \(2k + m\) bits. (If \(k = m\), then \(xr\) fits in \(3k\) bits.)

  8. The rest is straightforward: \(\left\lfloor \frac{xr}{4^k} \right\rfloor\) fits in \(m\) bits, \(\left\lfloor \frac{xr}{4^k} \right\rfloor n\) fits in \(2m\) bits and is in the range \([0, n^2)\), and \(t\) fits in \(m + 1\) bits.

Note: For extra optimization, the product \(\left\lfloor \frac{xr}{4^k} \right\rfloor n\) only needs \(m + 1\) low-order bits to be computed. This is because the next computed value \(t = x - \left\lfloor \frac{xr}{4^k} \right\rfloor n\) fits in \(m + 1\) bits, so there is no need to examine the upper \(m - 1\) bits of the product at all.

Comparison with Montgomery reduction

The Barrett algorithm and Montgomery reduction algorithm can both speed up modular reductions.

Similarities:

  • They both require precomputing various constants for a given modulus \(n\).

  • Their input range is \([0, n^2)\). It is useful for performing a reduction after multiplication, because with \(0 ≤ a, b < n\), we have \(0 ≤ ab < n^2\).

  • Their penultimate range is \([0, 2n)\), with a final fix-up step to reach the output range of \([0, n)\).

  • They perform 2 internal multiplications per reduction.

  • Their reduction phases avoid division or remainder by non-powers-of-2.

Differences:

  • Montgomery reduction requires numbers to be converted into and out of “Montgomery form” (expensive operations that require a true modulo operation in each direction), whereas Barrett reduction operates on regular numbers directly. This makes Montgomery reduction suitable for modular exponentiation but not for working with various unrelated numbers.

  • Montgomery is based on modular congruences and exact division, whereas Barrett is based on approximating the real reciprocal with bounded precision.

  • If the modulus is \(k\) bits long, then Montgomery internally performs two \(k\)-by-\(k\) bit multiplications yielding \(2k\) bits. But Barrett internally performs a \(2k\)-by-\(k\) bit multiplication yielding \(3k\) bits, plus a \(k\)-by-\(k\) bit multiplication yielding \(2k\) bits, so the Barrett algorithm is more expensive. (The bit lengths stated in this paragraph are slightly inexact, to within \(O(1)\).)

Source code

My Java implementation of Barrett reduction for int/long and BigInteger, with self-check and speed benchmark:

On x86 processors it appears that the native int64 modulo is as fast as Barrett reduction. The benchmark in SmallBarrettReducer shows both techniques being about the same speed. But on a CPU without a hardware divider, you might see Barrett reduction be measurably faster. For BigBarrettReducer, no benchmark is provided because the method BigInteger.modulo() is implemented quite fast.

A Python implementation with the full core algorithm but a less elaborate self-check is also available:

A short Mathematica program demonstrates the full computation, but doesn’t implement caching or data structures: