Project Nayuki

AVL tree list

Lists (or sequences) are a ubiquitous abstract data type (ADT) in computer science. The two classic ways to implement a list are the array and the linked list. While each one has its own advantages, each has some operations with the slow Θ(n) time complexity.

In most applications, it’s possible to use the appropriate data structure so that you only need to use the operations that have the fast Θ(1) time complexity and avoid the ones that take Θ(n) time. But in applications that require both fast random access and insertion/removal of elements anywhere in the list (especially in the middle), neither the array nor the linked list is appropriate.

By using a self-balancing tree structure – such as an AVL tree, red-black tree, or B-tree – it is possible to implement a list that can access and modify single elements in just Θ(log n) worst-case time, where n is the current size of the list.

Here is a summary of the trade-offs in time complexity:

Data structure Insert/remove
at beginning		 Insert/remove
at middle		 Insert/remove
at end		 Get/set
at middle
Array Θ(n) Θ(n) Θ(1) Θ(1)
Linked list Θ(1) Θ(n) Θ(1) Θ(n)
Balanced tree Θ(log n) Θ(log n) Θ(log n) Θ(log n)

Notes about the table:

  • This assumes the best implementation for a linked list, which would be a circular doubly linked list. A singly linked list with access only from the head would perform worse than what the table shows.

  • Array insertion at the end is Θ(1) if the array is pre-allocated with enough capacity. Otherwise it’s amortized Θ(1) (worst case Θ(n)) if it’s a dynamic array that needs to expand.

  • The time complexities for the balanced tree data structures are for the worst case per operation, not probabilistic or amortized. This behavior is better than skip lists, which have a probabilistically expected Θ(log n) time complexity.

Benchmark

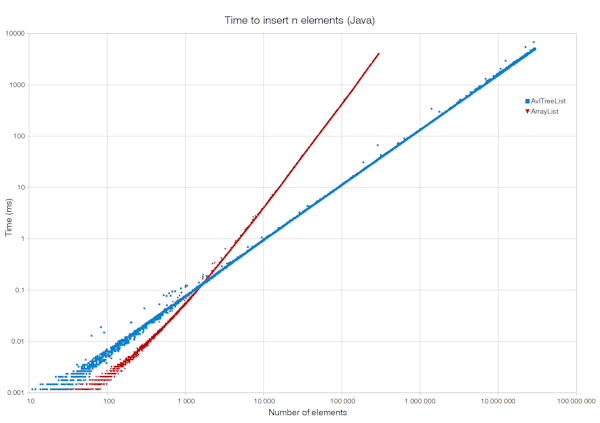
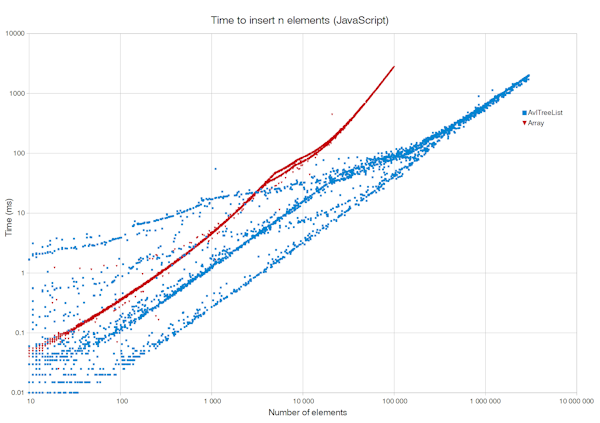
To demonstrate the power of the AVL tree list, we test a scenario that works badly for a dynamic array. We pick a size n, start with an empty list, and repeatedly insert an element into the current middle of the list n times. In Java code it would look like this:

List<Object> list = new AvlTreeList<>();
for (int i = 0; i < n; i++)
    list.add(i / 2, null);

The AVL tree list takes Θ(n log n) time to build up this list of n elements, whereas an array-based list takes a terrible Θ(n2) time to do the same task.

Java timings

JavaScript timings

Note: Java benchmarking was performed on Oracle Java 1.8.0 Update 45 (64-bit). JavaScript benchmarking was performed on Mozilla Firefox 46.0.1 (32-bit). The CPU was Intel Core i5-4690 (Haswell) 3.50 GHz and the OS was Windows 8.1 Pro (64-bit).

Source code

Java (SE 7+)

The class AvlTreeList implements java.util.List. You can use it as a drop-in replacement anywhere you use a List – though only rare situations need to use an AvlTreeList instead of the commonly used ArrayList. The iterator is not fail-fast unlike the ones in the Java collections framework. Take care to not modify the list when iterating over it.

Python

This implementation has an interface that mimics the built-in list type.

C++ (C++11 and above)

The class AvlTreeList has an interface similar to std::vector. Currently no iterator is implemented.

TypeScript / JavaScript

The class AvlTreeList has some methods that are idiosyncratic and some that imitate the native Array class. The full set of methods is: length, get(), set(), insert(), remove(), clear(), iterator(), toArray(), push(), shift(), pop(), slice(), splice(), forEach().

C# (.NET 4.0+)

The class AvlTreeList almost implements the System.Collections.Generic.IList<T> interface. It can be used as a substitute for the commonly used List<T>. Currently no iterator is implemented.

Rust

The struct AvlTreeList has an interface similar to std::vec::Vec<T>. A move iterator and an immutable reference iterator are supported.

License: MIT (open source)

One application idea for the AVL tree list is to be the backing store for a scrollable graphical user interface that displays many thousands of items and allows the user to insert/edit/remove any item in the list (kind of like Windows Explorer or a big photo collection organizer).

Notes

  • This topic is covered in Introduction to Algorithms (the CLRS textbook), in the chapter “Augmenting Data Structures”, in the section on dynamic order statistics and retrieval by rank. Wikipedia covers this topic as an order statistic tree.

  • The Θ(log n) time complexity for single-element operations can also be achieved in the average case using skip lists, but this is a probabilistic data structure compared to the absolute guarantees provided by balanced trees.

  • All 3 classes of data structures in the table require Θ(n) time to search for a value to find its index in the list, but the tree structures can be augmented to do search in Θ(log n) time in a complicated way: Add a second balanced tree that is sorted by value and contains pointers to nodes in the primary tree; add parent pointers to each node in the primary tree so that when given a node, it’s possible to compute the node’s index in the list.

  • This discussion is about the time complexity of single-element operations on a list ADT. It’s not clear how to insert a whole list into a list or remove a whole range in logarithmic time and also be able to access random elements in logarithmic time. This can be a research or implementation exercise for the reader.

  • Because the balanced tree only updates Θ(log n) nodes on every operation and the nodes don’t have parent pointers, it is possible to implement this in a pure functional programming language like Haskell; similarly in imperative languages it is possible to make a copy-on-write implementation so that no nodes are ever modified in place.

  • The Python package blist implements lists as balanced trees, just like my AVL tree list here.

  • The Apache Commons Collections library provides a TreeList class that achieves the same goals as my Java implementation.

More info