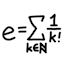Project Nayuki

Approximating Euler’s number correctly

Introduction

Suppose we want to calculate \(e\) (Euler’s number, Napier’s constant, 2.718281828...) accurate to 1000 decimal places. How can we do this from scratch with only big integer support, without the help of a computer algebra system?

The infinite series definition taught in introductory calculus is a good place to start at. But how many terms do we need to add up before truncating the series? How do we know the error bounds so that we can say for sure the result is correctly rounded? Do we need extra precision for intermediate calculations? Here is a sketch of some inadequate code:

double sum = 0.0;
double factorial = 1.0;
for (int i = 0; i < 99; i++) {  // When to terminate series?
    sum += 1 / factorial;  // How much error accumulated?
    factorial *= i + 1;    // Rounding error?
}

On this page we will go through the mathematics and algorithms to calculate \(e\) correctly from first principles, practical up to about 100 000 digits.

Basic definitions

Our basis will be the textbook definition of the number \(e\):

\( e \: = \: \displaystyle\sum_{k=0}^∞ \frac{1}{k!} \: = \: \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots . \)

Define the sequences of partial sums and remainders, for all \(n ∈ \mathbb{N}\):

\( S_n \: = \: \displaystyle\sum_{k=0}^n \frac{1}{k!} \: = \: \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \cdots + \frac{1}{n!} . \\ R_n \: = \: e - S_n \: = \: \frac{1}{(n + 1)!} + \frac{1}{(n + 2)!} + \frac{1}{(n + 3)!} + \cdots . \)

Main theorem

Because all the terms in the sum are strictly positive, it’s clear that every \(R_n > 0\).

Now let’s derive an upper bound on an arbitrary \(R_n\), assuming that \(n ≥ 1\):

\(\begin{align} R_n \: &< \: \frac{1}{(n + 1)!} + \frac{1}{(n + 1)! \: (n + 1)} + \frac{1}{(n + 1)! \: (n + 1)^2} + \cdots \\ &= \: \frac{1}{(n + 1)!} \left[ 1 + \frac{1}{n + 1} + \frac{1}{(n + 1)^2} + \cdots \right] \\ &= \: \frac{1}{(n + 1)!} \displaystyle\sum_{k=0}^∞ \frac{1}{(n + 1)^k} \\ &= \: \frac{1}{(n + 1)!} \frac{n + 1}{n} \: = \: \frac{1}{n! \: n} \\ &\leq \: \frac{1}{n!}. \end{align}\)

Explanations:

  • The first line is due to the definition of the factorial function, like \((n + 2)! = (n + 1)! \: (n + 2) > (n + 1)! \: (n + 1)\), etc.

  • The second line is by factoring like terms.

  • The third line rewrites the infinite sum formally.

  • The fourth line is due to the well-known geometric series.

  • The fifth line weakens the inequality (because \(0 < \frac{1}{n} ≤ 1\)), which will simplify the computation later on.

In summary, we have for every \(n ≥ 1\):

\( 0 \: < \: R_n \: < \: \frac{1}{n!}. \)

Add \(S_n\) to all sides to get:

\( S_n \: < \: S_n + R_n = e \: < \: S_n + \frac{1}{n!}. \)

Or negate the inequality and add \(e\) to get:

\( e - \frac{1}{n!} \: < \: S_n \: < \: e. \)

In other words, when truncating the infinite series for \(e\) after \(n+1\) terms (i.e. the last term is \(\frac{1}{n!}\)), this partial sum \(S_n\) is strictly less than \(e\), but differs from \(e\) by no more than \(\frac{1}{n!}\).

The main idea in the algorithms described below is that when both \(S_n\) and \(S_n + \frac{1}{n!}\) are rounded to the same value, we can be sure this is the correct approximation of \(e\). Otherwise we continue adding terms to the partial sum and wait for the difference between these two values to shrink.

Fraction algorithm

This algorithm follows fairly straightforwardly from the mathematical argument, with \(m\) being the number of decimal places we want to calculate:

  1. Start with \(n = 0\).

  2. (Top of loop) Calculate the partial sum \(S_n\) as an exact fraction.

  3. Consider the inequality \(S_n < e < S_n + \frac{1}{n!}\), which says that the true value of \(e\) lies within an interval of length \(\frac{1}{n!}\). If the interval length exceeds \(10^{-m}\) then the lower and upper ends of the interval round to different numbers, so no answer is available.

  4. If \(\frac{1}{n!} < 10^{-m}\), then we check whether \(\text{round}(S_n) = \text{round}(S_n + \frac{1}{n!})\). If equal, then exit the loop and return \(\text{round}(S_n)\) as the result.

  5. Otherwise increment \(n\) and loop again.

If your programming language doesn’t have a library for fractions / rational numbers, it’s not a problem because the functionality can be implemented in a few dozen lines of code.

Unfortunately, the fractions get big quickly because the denominator is \(n!\). In practice, this algorithm takes about 20 seconds to compute 3 000 decimal places on my computer, which is hardly impressive.

Source code:

Interval algorithm

Instead of calculating the partial sum and each term using exact fractions, let’s approximate them by using closed intervals (i.e. \([\text{low}, \text{high}]\)) to represent where the true value must reside.

The key idea of this algorithm is to use fixed-point arithmetic with {\(m\) plus an extra \(p\)} decimal places of precision, along with interval arithmetic to bound the uncertainty. So for the low end we round calculations down, and for the high end we round calculations up. This procedure is a refinement of the fraction algorithm with added complexity:

  1. Start with \(n = 0\), \(\text{sum} = [0, 0]\), \(\text{term} = [10^{m+p}, 10^{m+p}]\).

  2. (Top of loop) Let \(\text{sum} = [\text{sum}_L + \text{term}_L, \: \text{sum}_H + \text{term}_H]\).

  3. Because \(\frac{10^{m+p}}{n!} ∈ [\text{term}_L, \text{term}_H]\), we know that \(\text{sum}_L < e < \text{sum}_H + \text{term}_H\).

  4. If \(\text{term}_H < 10^p\) (analogous to \(\frac{1}{n!} < 10^{-m}\)), then it may be possible to generate a result. In particular, if \(\text{round}(\text{sum}_L) = \text{round}(\text{sum}_H + \text{term}_H)\), then we return this as the result.

  5. Otherwise increment \(n\), let \(\text{term} = [\lfloor \text{term}_L / n \rfloor, \: \lceil \text{term}_H / n \rceil ]\), and loop again.

This algorithm is much faster than the fraction-based algorithm, taking about 20 seconds on my computer to get 100 000 decimal places (30× more digits for the same time spent).

Actually, step 5 can lead to a number of simplifications:

  • Truncating division is available but ceiling division usually isn’t, so we can be lazy by setting \(\text{term}_H = \lfloor \text{term}_H / n \rfloor + 1\) (since pessimistically \(\lceil x \rceil ≤ \lfloor x \rfloor + 1\)).

  • We can be lazier and more pessimistic by fixing \(\text{term}_H = \text{term}_L + n + 1\) (because \(n\) floor operations were performed, and each division by a positive integer does not increase the error).

  • Finally, we can be laziest by fusing \(\text{term}_H\) into \(\text{sum}_H\) by always letting \(\text{sum}_H = \text{sum}_L + \frac{n(n+1)}{2}\) (due to the arithmetic series).

Source code:

The exponential function

We can extend this analysis and approximate the exponential function using the same line of reasoning. For simplicity, assume that \(x > 0\). Recall the standard definition:

\(\exp(x) \: = \: \displaystyle\sum_{k=0}^∞ \frac{x^k}{k!} \: = \: \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots . \)

Define the partial sums and the remainders in the same way, for all \(n ∈ \mathbb{N}\):

\( S_n(x) \: = \: \displaystyle\sum_{k=0}^n \frac{x^k}{k!} \: = \: \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + \cdots + \frac{x^n}{n!} . \\ R_n(x) \: = \: \exp(x) - S_n(x) \: = \: \frac{x^{n+1}}{(n + 1)!} + \frac{x^{n+2}}{(n + 2)!} + \frac{x^{n+3}}{(n + 3)!} + \cdots . \)

It should be clear that \(R_n(x) > 0\) for all \(x > 0\) and \(n ∈ \mathbb{N}\).

Now let’s derive the main inequality, assuming that we pick an integer \(n\) such that \(n > x\):

\(\begin{align} R_n(x) \: &< \: \frac{x^{n+1}}{(n + 1)!} + \frac{x^{n+2}}{(n + 1)! \: (n + 1)} + \frac{x^{n+3}}{(n + 1)! \: (n + 1)^2} + \cdots \\ &= \: \frac{x^{n+1}}{(n + 1)!} \left[ 1 + \frac{x}{n + 1} + \frac{x^2}{(n + 1)^2} + \cdots \right] \\ &= \: \frac{x^{n+1}}{(n + 1)!} \displaystyle\sum_{k=0}^∞ \left( \frac{x}{n + 1} \right)^k \: = \: \frac{x^{n+1}}{(n + 1)!} \frac{n + 1}{n + 1 - x} \\ &= \: \frac{x^{n+1}}{n! \: (n + 1 - x)} < \: \frac{x^{n+1}}{n!}. \\ \end{align}\)

Therefore we have:

\(0 < R_n(x) < \displaystyle \frac{x^{n+1}}{n!}. \\ S_n(x) < \exp(x) < S_n(x) + \displaystyle \frac{x^{n+1}}{n!}.\)

Here is the program based on the interval algorithm. Source code:

Notes

  • These algorithms work for any rounding mode as long as the rounding is a monotonic function. For example, floor, ceiling, truncation, and round-half-to-even are all acceptable.

  • I tried to be fairly rigorous and explicit in the mathematical analysis, though I did omit most of the basic algebra.

  • The other textbook definition of \(e = \displaystyle\lim_{n \to ∞} \left( 1 + \frac{1}{n} \right)^n\) is not useful for computational purposes.

  • The algorithms described by me here are nowhere near the state of the art. A casual look at the list of records shows that it’s quite reasonable to compute billions of digits of \(e\).

  • There is no guarantee that my algorithms, or anyone else’s algorithms terminate. This is because the value being computed could be very close to a rounding boundary, like in the case of 1.499999999992. However, the chance of this happening for a “nice” number like \(e\) (which is irrational and possibly normal) is exceedingly small, so this is not a concern in practice.

  • Computing \(\exp(x)\) for large \(x\) requires a lot of extra precision. I am aware of this problem but have no solution to offer.

  • Handling the \(x < 0\) case is left as an exercise to the reader. It’ll be somewhat uglier because the sum has positive and negative terms.

  • My formulas and inequalities for approximating \(e\) have a lot in common with a proof that \(e\) is irrational.

  • Easy-to-follow ideas for speeding up the calculation: Brothers Technology: Improving the Convergence of Newton’s Series Approximation for e