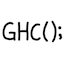A math/programming view of Canada GST/HST credit calculation

Introduction

As a programmer and mathematician, I like to go beneath the surface of everyday activities to find and understand the math and logic hidden inside. When I was preparing my Canadian income tax returns, I couldn’t help but notice that the calculations in the tax forms were a form of math and programming expressed in a different notation. So I want to explore what would happen if I recast these calculations in math notation and code, and from there on apply standard techniques for manipulating and analyzing the logic (e.g. algebra and graphing).

In this article, I will illustrate using the real-life example of the Canadian GST/HST credit calculation form, for tax year 2012 (payable in mid-2013 to mid-2014), focusing on chart 2 (for an unmarried person with no children, which has the simplest calculation). The official version of the form, with copious instructions and definitions, are found here:

PDF: http://www.cra-arc.gc.ca/E/pub/tg/rc4210/rc4210-13e.pdf (preferred for better formatting)
HTML: http://www.cra-arc.gc.ca/E/pub/tg/rc4210/rc4210-e.html

$Canada GST/HST credit - 2012 - Chart 2$

Expressed as program code

As a side note, we could take the form and re-implement it in a spreadsheet (e.g. Excel), and it would look and behave identically to the original form. (This is left as an exercise for the reader.) The advantage is that you can execute the logic automatically on a computer and be able to try different input values with ease. But this technique is not so interesting to me, so we’ll skip it and start with a real programming language.

If we work through the form line by line and write Java code as literally as possible, this is what we get (31 lines, public domain):

double calculateGstHstCreditChart2(
        double netIncome, double adjustedNetIncome) {
    
    double line1 = 265.00;
    
    double line7;
    if (netIncome > 8608.00) {
        double line2 = netIncome;
        double line3 = 8608.00;
        double line4 = line2 - line3;
        double line5 = 0.02;
        double line6 = line4 * line5;
        line7 = Math.min(line6, 139.00);
    } else {
        line7 = 0.00;
    }
    double line8 = line1 + line7;
    
    double line13;
    if (adjustedNetIncome > 34561.00) {
        double line9  = adjustedNetIncome;
        double line10 = 34561.00;
        double line11 = line9 - line10;
        double line12 = 0.05;
        line13 = line11 * line12;
    } else {
        line13 = 0.00;
    }
    double line14 = line8 - line13;
    
    return line14;
}

By translating from instructions written in English (a human natural language) to code in a real programming language, we immediately gain two useful properties. The instructions in the natural language are written in an ad hoc way, using a variety of wording and logic constructs. It’s difficult to ensure that every calculation form is understandable and unambiguous (see the notes for an example of ambiguity). Contrast this with the program code, where every operation has a clear definition, leaving no room for ambiguity.

Obviously, we can run the code on a computer to test its behavior and check its results. Computers are very fast, and we can run this calculation on millions of cases per second if we so desired. (In fact, if we had a database of the income of every person in Canada (about 35 million), we can easily run this function on every person, taking only a few seconds in total. That’s right, it’s entirely feasible to process an entire nation’s worth of data on a single personal computer – though it depends on the type of calculation.)

A standard code simplification technique is that if a variable is used only once, then its definition can be inlined into the place where it is used. Here we have numerous opportunities to do inlining, and it would significantly shorten the code. For example, in the first if-statement, the 6 lines of the body can be condensed to simply: line7 = Math.min((netIncome - 8608.00) * 0.02, 139.00);. For typical programmers, a line of code with this amount of complexity is actually considered quite simple, taking not much mental effort to process. It could be argued that the calculation can be split into 2 lines, but definitely any more than 2 would be too verbose and harmful for readability. After fully inlining all the variables and doing small tweaks to the logic, this is the much-simplified code that we get:

double calculateGstHstCreditChart2(
        double netIncome, double adjustedNetIncome) {
    
    double total = 265.00;
    if (netIncome > 8608.00)
        total += Math.min((netIncome - 8608.00) * 0.02, 139.00);
    if (adjustedNetIncome > 34561.00)
        total -= (adjustedNetIncome - 34561.00) * 0.05;
    return total;
}

We can clearly see the input-output relationship in the function: It takes two input numbers named netIncome and adjustedNetIncome, and it calculates one output number. This is useful to know because the information is complete, so we can draw conclusions about the non-relationships: for example, this calculation does not depend on the number of children (input), does not determine your provincial tax credit (output), does not involve your RRSP amounts, etc. Being able to identify the scope of the calculation helps to clarify the big picture.

Expressed as a math formula

For the notation, line i is denoted as $L_i$, and input variables are written as acronyms (namely $NI$ and $ANI$).

First, we need to get rid of those unnatural if-statements. Observe that we can rewrite $L_7$ and $L_{13}$ to use $\max(\dots, 0)$ instead: For example, regarding $NI$ and $L_7$, if $NI < 8608$ then we can pretend $NI = 8608$, so the long computation will still yield $L_7 = 0$ as wanted. The same reasoning goes for $ANI$ and $L_{13}$. Other than this consideration, we simply do repeated substitution of variables until the formula depends only on the input variables.

$L_{14} = L_8 - L_{13} \\ = (L_1 + L_7) - (L_{11} × L_{12}) \\ = (265 + \min(L_6, 139)) - ((L_9 - L_{10}) × 0.05) \\ = (265 + \min(L_4 × L_5, 139)) - ((\max(ANI, 34561) - 34561) × 0.05) \\ = (265 + \min((L_2 - L_3) × 0.02, 139) - ((\max(ANI, 34561) - 34561) × 0.05) \\ = (265 + \min((\max(NI, 8608) - 8608) × 0.02, 139) - ((\max(ANI, 34561) - 34561) × 0.05) \\ = 265 + \min(0.02(\max(NI, 8608) - 8608), 139) - 0.05(\max(ANI, 34561) - 34561).$

We have thus condensed the entire form into a one-line formula:

$GHC(NI, ANI) = 265 + \min(0.02(\max(NI, 8608) - 8608), 139) - 0.05(\max(ANI, 34561) - 34561)$,

where $GHC$ is the GST/HST credit, $NI$ is the net income, $ANI$ is the adjusted net income, and all variables denote monetary amounts in Canadian dollars.

Mathematical analysis

For the purposes of analysis, let’s simplify the problem by assuming that $ANI = NI$. (The actual ANI requires a couple of calculations.) This may or may not introduce significant inaccuracies, but we just want to get a rough idea for how the GST/HST credit varies with a person’s net income.

Taking the function in the previous section, setting $ANI = NI$, renaming $NI$ to $x$, and renaming $GHC$ to $f$, we get:

$f(x) = 265 + \min(0.02(\max(x, 8608) - 8608), 139) - 0.05(\max(x, 34561) - 34561)$.

Graphing

We can plot the function with a suitable tool like Wolfram|Alpha, a computer algebra system like Mathematica/Maple/Maxima, a graphing calculator, etc.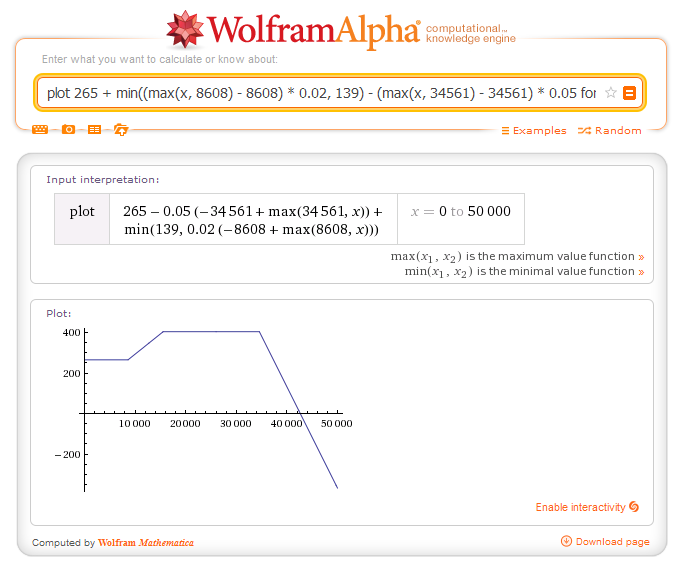

$GST/HST credit graph in Wolfram|Alpha$

The original form offered little insight about how income is related to the credit, but now the graph shows these facts as clear as day:

The maximum credit is about $400 (in fact, exactly $404), which is attained for incomes of about $15 000 to $35 000.
The credit goes to zero when the income goes to about $42 000, so there is no point in applying for the credit above this income level.
In fact, the calculation allows the credit to become negative if the income is much above $40 000. Despite this logic, the actual credit would be $0. You would not be expected to pay money back – this is supposed to be just “common sense” but is not expressed explicitly in the calculation logic.
The relationship between the input and output is a continuous function, so there are no sudden jumps as the income changes.

Piecewise definition

With some algebraic manipulation (not shown), we can conclude that the function is continuous and piecewise-linear, and we can rewrite it equivalently as a piecewise definition:

$f(x) = \begin{cases} 265 &, \; \text{if } x \leq 8608 \\ 265 + 0.02(x - 8608) &, \; \text{if } 8068 < x < 15558 \\ 404 &, \; \text{if } 15558 \leq x \leq 34561 \\ 404 - 0.05(x - 34561) &, \; \text{if } x > 34561 \end{cases}$.

When expressed in this format, it’s much easier to evaluate the function by hand because it doesn’t use parenthesized expressions or min/max. Also, it’s easy to calculate the derivative of the function, which tells you how the GST/HST credit amount changes as the net income increases.

Final thoughts

I do computer programming as a job and as a hobby, and though I regularly write code that’s far more complex and subtle than the example here, I always appreciate and strive for simplicity. My gut feeling after dissecting these calculations is that they’re too complex for the goal of fair and socially desirable taxation – there must be a simpler way to achieve this without having an explicit GST/HST credit calculation. It can perhaps be folded into the income tax calculation and UCCB. But the tax code (and laws in general) generally works in the direction of accreting complexity and rarely shedding it, so this idea is unlikely to happen. It seems that simplifying a bunch of overlapping or conflicting laws, or removing rare or obsolete laws, takes much more effort than adding a new law. Needless to say, I don’t have high hopes for the tax code becoming simpler in the future.

While the GST/HST credit calculation by itself costs a small amount of effort, when it’s combined with all the other calculations in preparing an income tax return, the burden quickly adds up. (For example, I have dealt with Schedule 11 for tuition credits and form T2209 for foreign tax credits, just to name a few.) Complexity has a real human cost in numerous ways. Instructions that are difficult to understand, non-standard, or simply long will confuse users. Complexity increases the chance of (human) errors and exacerbates the consequences of errors, such as time wasted in explaining and resolving them, effort in interpreting and auditing numbers, general bureaucracy and red tape, and loss of goodwill. And no, “complexity creates jobs for tax accountants” is a poor excuse – it would be like saying that digging holes and filling them in “creates jobs for construction workers”; it’s better to avoid creating complexity in the first place and let people enjoy other things in life than tax calculations.

Paradoxically, this GST/HST credit calculation form is not as intimidating as it looks, yet at the same time it’s more intimidating than it looks. It’s not so intimidating because once you know how to do the calculations, you can be confident that you can do it correctly every time, even if the instructions are long. On the other hand, even though the calculation steps are shown plainly in front of you, the implications behind those calculations (such as a graph) are not obvious at all; the meaning is obscured by the syntax and the sheer tedium of working line by line instead of using a more compact, powerful notation. From this exercise, we can see that the ad hoc spreadsheet-like notation used by the CRA is an inefficient and inferior notation compared to standard math notation, and fails to take advantage of the fact that learning algebra and functions is mandatory in Canadian high schools.

Notes

The government provides an online calculator to help you calculate your GST/HST credit. But it’s rather tedious to use, involving a dozen questions spanning multiple pages. It also doesn’t calculate the same quantity; the form calculates the annual credit while the online calculator calculates the quarterly credit payment.
You could argue that this exercise was pointless because to apply for the GST/HST credit, you simply need to tick a checkbox in your income tax return, then the calculations are done for you entirely by the government. But having transparent rules is important, which means you want to be able to calculate the amount for yourself. Moreover, this form was intended to serve as a representative example – many other tax forms have similar logic and similar problems with ambiguity/verbosity/etc.
I chose Java for the illustrative example because it’s my preferred language, but the code above can be straightforwardly adapted to C, JavaScript, Python, BASIC, etc. Speaking from experience, translating from the human language form to a programming language is the hard part because it requires interpretation of the wording, detecting ambiguity/errors, and carefully considering the consequences of each calculation. By comparison, translating from one programming language to another is entirely mechanical and unambiguous.
Strictly speaking, these calculations in the Java code should be performed using BigDecimal and rounded after every calculation. But for the purposes of this article, the simplicity of using binary floating-point is sufficient.
Chart 3 seems to have an ambiguity, where one phrase can be interpreted in multiple conflicting ways. Line 3 pertains to the “credit for your other children”, but it asks you to multiply your “number of children” by $139.00 instead of multiplying (your number of children minus 1) by $139.00. It also has a special “credit for your first child” in line 2, which suggests that the first child should be excluded from line 3. The HTML version of the form makes this situation very ambiguous. However, in the PDF form, it’s fairly clear by the context of the indentation that the “number of children” indeed means the “number of other children”. The code version precisely prevents this kind of ambiguity that requires careful interpretation, common sense, and attention to context.