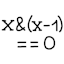 Some bit-twiddling functions explained
Some bit-twiddling functions explained
Introduction
Using clever bitwise arithmetic, it’s possible to implement some useful arithmetic functions in a short amount of code without using expensive loops or branches (if-statements). Here I will give some bit-twiddling functions expressed in the Java programming language and give proofs to justify their correctness.
For those who are unfamiliar with the specifics of Java but know another programming language well:
The syntax for statements and expressions is essentially the same as that in C, C++, C#, D, JavaScript, etc.
intis a signed 32-bit two’s complement integer type.Integer overflow is silent and well-defined (unlike C/C++).
The
>>operator means signed (arithmetic) right shift, and>>>means unsigned (logical) right shift.It is not easy to translate these pieces of Java code correctly into C or C++, due to complications involving overflow undefined behavior, signed/
unsigned type conversions, and sign-magnitude and ones’ complement arithmetic.
Absolute value
Naive version:
int abs(int x) {
if (x >= 0)
return x;
else
return -x;
}
Bit-twiddling version:
int abs(int x) {
int y = x >> 31;
return (x + y) ^ y;
}
How this implementation works is as follows: y is the sign bit of x replicated to all 32 bits. If x >= 0, then y == 0, and (x + 0) ^ 0 == x. Otherwise x < 0, which means bit #31 of x is 1, so y == 0xFFFFFFFF. By definition since x has the type int, we have ~x == (x ^ 0xFFFFFFFF). By the definition of two’s complement arithmetic, -x == (~x) + 1 == ~(x - 1). With y == -1, we have (x + y) ^ y == ~(x + (-1)) == ~(x - 1) == -x.
The expression being returned can be written equivalently as: (x ^ y) - y. The proof is left as an exercise to the reader.
Take note of one caveat: The most negative number, Integer.MIN_VALUE = −231 = −2147483648, does not have a positive counterpart. But this implementation gives abs(Integer.MIN_VALUE) == Integer.MIN_VALUE, much like Math.abs(int), instead of throwing an exception.
Sign function
Naive version:
int sign(int x) {
if (x > 0)
return +1;
else if (x < 0)
return -1;
else
return 0;
}
Bit-twiddling version:
int sign(int x) {
return (x >> 31) | ((-x) >>> 31);
}
To show why this implementation of the sign function is correct, consider the three cases:
If
x == 0: Left side is(x >> 31) == 0. Right side is-x == 0,((-x) >>> 31) == 0. Finally,(0 | 0) == 0.If
x > 0: Left side, the top bit (bit #31) is 0, so(x >> 31) == 0. Right side, the top bit of-xis 1 because every positiveinthas a negative counterpart, so((-x) >>> 31) == 1. Finally,(0 | 1) == 1.If
x < 0: Left side, the top bit (bit #31) is 1, so(x >> 31) == 0xFFFFFFFF == -1. Right side, we can disregard the value. Finally,(-1 | anything) == -1.
Power-of-2 test
Naive version:
boolean isPowerOf2(int x) {
for (int i = 0; i <= 30; i++) {
if ((1 << i) == x)
return true;
}
return false;
}
Bit-twiddling version:
boolean isPowerOf2(int x) {
return x > 0 && (x & (x - 1)) == 0;
}
This function returns true if x ∈ {1, 2, 4, 8, 16, ..., 1073741824} but false otherwise. To start, the condition x > 0 excludes numbers that cannot possibly be a non-negative integral power of 2. Now consider two cases:
If
xis a power of 2, thenxhas a leftmost 1 followed by zero or more 0s. Withx == binary 1 (n 0s), we know thatx - 1 == binary 0 (n 1s). Since inxandx - 1the 1s are in different positions, their bitwise conjunction is zero:(x & (x - 1)) == 0.If
x > 0andxis not a power of 2, thenxhas a leftmost 1 and some other 1 to the right of it. That is, the position ofx’s rightmost 1 is different than the position of the leftmost 1. So the number has a form:x == binary 1 dddd 1 0...0, whereddddrepresents zero or more digits of any value. Thenx - 1 == binary 1 dddd 0 1...1, where the right part 10...0 turns into 01...1. The left part 1dddd is unchanged, thus(x & (x - 1)) == binary 1 dddd 00...0 != 0.
Set nonzero to all ones
Naive version:
int isNonzero(int x) {
if (x == 0)
return 0x00000000;
else
return 0xFFFFFFFF;
}
Bit-twiddling version:
int isNonzero(int x) {
return (x | (-x)) >> 31;
}
Proof of correctness:
If
x == 0, then clearly(0 | (-0)) >> 31 == (0 | 0) >> 31 == 0 >> 31 == 0.If
x > 0, then-xis a negative number where bit #31 is 1. Hencex | (-x)still has the top bit set to 1, and(x | (-x)) >> 31 == 0xFFFFFFFF == -1.If
x < 0, thenxhas bit #31 set to 1. Hencex | (-x)has the top bit set to 1, and reduces to the previous case.
This simple function serves as a useful building block for expressing conditional statements that can be evaluated in constant time regardless of input values. Constant-time execution is important in the implementation of cryptographic primitives (e.g. ciphers, bigint arithmetic) because variations in timing could disclose information about secret inputs (e.g. keys, messages). I applied tricks similar to this isNonzero() function in my Bitcoin cryptography library, especially in the implementation of ECDSA such as in Int256Math.java.
More info
- Bit Twiddling Hacks
- Hacker’s Delight (traditional book), table of contents