Project Nayuki

Reference Huffman coding

This project is a clear implementation of Huffman coding, suitable as a reference for educational purposes. It is provided separately in Java, Python, and C++, and is open source (MIT License).

The code can be used for study, and as a solid basis for modification and extension. Consequently, the codebase optimizes for readability and avoids fancy logic, and does not target the best speed/memory/performance.

Source code

The files in this project are available in Git repositories:

Web host Browse files Download package
GitHub (primary) Browse files Download ZIP
GitLab (mirror) Browse files Download ZIP

Overview

Huffman encoding takes a sequence (stream) of symbols as input and gives a sequence of bits as output. The intent is to produce a short output for the given input. Each input yields a different output, so the process can be reversed, and the output can be decoded to give back the original input.

In this software, a symbol is a non-negative integer. The symbol limit is one plus the highest allowed symbol. For example, a symbol limit of 4 means that the set of allowed symbols is {0, 1, 2, 3}.

Submodules

Submodule dependency graph
Sample applications

Two pairs of command-line programs fully demonstrate how this software package can be used to encode and decode data using Huffman coding. One pair of programs is the classes HuffmanCompress and HuffmanDecompress, which implement static Huffman coding. The other pair of programs is the classes AdaptiveHuffmanCompress and AdaptiveHuffmanDecompress, which implement adaptive/dynamic Huffman coding.

Encoder/decoder

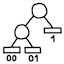
The classes HuffmanEncoder and HuffmanDecoder implement the basic algorithms for encoding and decoding a Huffman-coded stream. The code tree must be set before encoding or decoding. The code tree can be changed after encoding or decoding each symbol, as long as the encoder and decoder have the same code tree at the same position in the symbol stream. At any given time, the encoder must not attempt to encode a symbol that is not in the code tree.

Code tree model
Huffman code tree

The class CodeTree, along with Node, InternalNode, and Leaf, represent a Huffman code tree. The leaves represent symbols. The path to a leaf represents the bit string of its Huffman code.

Frequency table

The class FrequencyTable wraps over a simple integer array to count symbol frequencies. It is also responsible for generating a Huffman code tree that is optimal for its current array of frequencies (but not necessarily canonical).

Canonical codes

The class CanonicalCode converts an arbitrary CodeTree to a canonical code. It can then generate a CodeTree for the canonical code.

Bitwise I/O streams

The classes BitInputStream and BitOutputStream are bit-oriented I/O streams, analogous to the standard bytewise I/O streams. However, since they use an underlying bytewise I/O stream, the bit stream’s total length is always a multiple of 8 bits.

Test suite

A JUnit test suite checks that compressing and decompressing an arbitrary byte sequence will give back the same byte sequence. This is done on short, simple sequences and on longer random sequences. The test suite checks the 4 main programs mentioned above (HuffmanCompress, etc.).

Other languages

The Python and C++ versions of this library were ported from the Java version. They contain all the core functionality provided by the Java version, but not some of the extended features or verbose documentation comments. The API naming and semantics follow the Java version, unless the target language has a more idiomatic way of doing things (e.g. underscore names and native bigint in Python). All language versions encode and decode exactly the same data. For example, it is acceptable to encode a file using HuffmanCompress.java and then decode it using huffman-decompress.py.

Limitations

  • The code is optimized for understandability, not performance. For example, the Java CodeTree uses memory grossly inefficiently to store the code bit string for each symbol. It uses ArrayList<Integer> at a cost of at least 4 bytes per represented bit, instead of packing bits into a primitive integral array type such as byte[].

  • CodeTree, FrequencyTable, and CanonicalCode explicitly take a symbol limit as a parameter. This is not strictly required, but the alternative is to use sparse tables, which is more difficult to understand.

  • A couple of methods use recursion to traverse a whole code tree. When using such a method on a deep tree, a StackOverflowError may be thrown.

  • All the Huffman-related code only work with alphabets with up to Integer.MAX_VALUE (i.e. 231 − 1) symbols in the Java version, and up to UINT32_MAX (i.e. 232 − 1) symbols in the C++ version.

  • FrequencyTable can only track each symbol’s frequency up to Integer.MAX_VALUE in Java and UINT32_MAX in C++. Trying to increment a symbol’s frequency beyond this limit raises an exception. However, using frequencies larger than 231 should be rare in practice.

Suggestions

Here are some suggestions on how to use, modify, or extend this software:

  • Extract an interface from the bitwise I/O streams and create other concrete implementation classes.

  • Improve the speed of Huffman encoding and decoding. One advanced suggestion is to treat the Huffman decoder as a finite-state machine (FSM) and decode a whole byte per iteration.

  • Layer another encoding scheme on top of Huffman coding, such as RLE, LZW, n-gram models, DCT with quantization, etc. This is essentially how real-world compressed data formats are structured.

More info