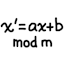Fast skipping in a linear congruential generator

Introduction

The LCG is perhaps the simplest pseudorandom number generator (PRNG) algorithm. The generator’s state consists of a single integer, and each step involves a multiplication, addition, and modulo operation. The behavior of an LCG is defined by the following recurrence relation:

$\begin{align} x_0 &= \text{seed}. \\ x_{n+1} &≡ (a x_n + b) \text{ mod } m \text{, for all $n ∈ \mathbb{N}$}. \end{align}$

The integer constants $a$, $b$, $m$ are chosen carefully to give good properties. For example: having a full period of $m$, having $m$ be a power of 2 (which is efficient on computers), and/or having $b$ be 0 (to save an operation). The seed value can be chosen (almost) arbitrarily for each random number generator instance. The sequence of values $x_0, x_1, x_2, \ldots, x_n, \ldots$ represents the pseudorandom outputs from the generator. These values can be used as is, or they can be filtered and have their distribution altered.

Fast skipping

Suppose we know $x_0$ and we want to determine $x_n$ for some $n ∈ \mathbb{N}$. Clearly it is possible to iterate the recurrence formula $n$ times to get our desired result, which takes $\Theta(n)$ time. But with some clever arithmetic, we can get the result much faster, in only $\Theta(\log n)$ time.

First, consider the special simple case where $b = 0$. Then $x_n ≡ a^n x_0 \text{ mod } m$. We can compute $a^n x_0 \text{ mod } m$ quickly using the well-known modular exponentiation algorithm, which is exponentiation by squaring with a reduction of each intermediate result modulo $m$.

Now for the general case, consider the LCG recurrence relation without the modulo and with $x ∈ \mathbb{R}$:

$x_{n+1} = a x_n + b \text{, for all $n ∈ \mathbb{N}$}$.

This first-order linear recurrence has a closed-form solution^[0] :

$x_n = a^n x_0 + \frac{a^n - 1}{a - 1} b$.

Reinsert the modulo and propagate it inward to get:

$x_n ≡ \left[(a^n x_0 \text{ mod } m) + \left(\frac{a^n - 1}{a - 1} b\right)\right] \text{ mod } m$.

The first term, $a^n x_0 \text{ mod } m$, is the modular exponentiation discussed earlier.

The second term is trickier. The quotient $\frac{a^n - 1}{a - 1}$ is always an integer, because it is equal^[1] to $a^{n-1} + a^{n-2} + \cdots + a^1 + a^0$. To compute $\frac{a^n - 1}{a - 1} \text{ mod } m$, we compute $(a^n - 1) \text{ mod } (a - 1) m$, then non-modular-divide^[2] by $a - 1$. (If $a-1$ is coprime with $m$, then we also have the alternative of multiplying by $(a-1)^{-1} \text{ mod } m$.)

Putting these facts together, we finally have:

$x_n ≡ \left[\left(a^n x_0 \text{ mod } m\right) + \left(\frac{(a^n - 1) \text{ mod } (a -1) m}{a - 1} b\right)\right] \text{ mod } m$.

Backward iteration

By rearranging the recurrence relation to solve for the other variable, we get:

$x_n \: ≡ \: a^{-1} (x_{n+1} - b) \: = \: a^{-1} x_{n+1} + (a^{-1})(-b) \mod m$.

As long as $a$ and $m$ are coprime, the multiplicative inverse of $a$ exists and can be computed by the extended Euclidean algorithm.

The formula above calculates one step backward. We can do fast backward skipping using the forward formula, but replacing its $a$ variables to $(a^{-1} \text{ mod } m)$ and its $b$ variables to $(-(a^{-1} b) \text{ mod } m)$.

Source code

The fast skipping and backward iteration concepts discussed in the text are implemented in the following runnable programs:

Java version: LcgRandom.java
Python version: lcgrandom.py

Notes

[0]: Finding this closed-form solution requires some ingenuity, a table of algebraic expansions, or a computer algebra system (CAS). But now that the solution has been stated, you can prove its correctness by induction quite easily.
[1]: Proof of $\displaystyle\frac{a^n - 1}{a - 1} = \sum_{i=0}^{n-1} a^i $ is left as an exercise for the reader.
[2]: This operation is correct if we revisit the definition of the modulus operator: $r = x \text{ mod } m$ finds the unique pair of integers $q$ and $r$ such that $0 ≤ r < m$ and $x = qm + r$.